刚刚接触双连通分量,比较纠结,记录下来防止遗忘。
转自 http://www.haogongju.net/art/1330869
1:一些概念
割点:是无向连通图中一个顶点v, 如果删除它以及它关联的边后,得到的新图至少包含两个连通分支。
桥:无向连通图中的一条边,如果删除它,得到的新图包含两个连通分量。
双连通图:不含割点的无向连通图。
双连通分支:无向连通图的最大双连通子图。
点双连通分支:(自己猜的)通过找割点获得的双连通分支。
边双连通分支:(自猜)通过找桥获得的双连通分支。
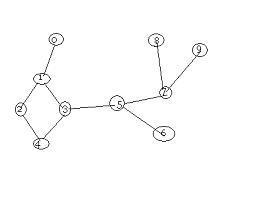
举个例子:一个无向图有 1、2、3、4、5共5个顶点,一共有如下6条边,1 2,2 3,1 3,34,3 5,45,由于去掉任意一条边原图都是连通的,所以原图整体是边双连通的,但3是一个割点,如果去掉3原图就不连通了,所以原图整体不是点双连通的。还有是在有重边的情况下,边连通和点连通有点区别。
2:思路:tarjan算法
用dfs搜索整个图,用dfn[]记录节点搜索到的时间,low[]记录从该节点能够通过树边和反向边到达的最早搜索到的节点。(注意,这里的反向边(连接到dfs搜索树祖先的边)不考虑反向连接父亲的那条边,因为无向图的边会变成两个方向的边)
对于强连通分量,对每个节点u DFS,遇到一个没有访问过的节点v即dfn[v] ==0,则继续递归搜索tarjan(v),之后重置low[u] = min(low[u],low[v]);如果遇到的是之前访问过的节点v(在栈中的,由于存在横插边,需要mark[]记录节点是否在栈中),则直接重置low[u]= min(low[u], dfn[v])。当节点u的所有儿子访问完成判断u节点是否为根节点(low[u] ==dfn[u]),其表示u之后的节点不能通过后向边到达u之前,取出强连通分量则用栈存节点。
要求双联通分支,先要知道割点和桥的求法。
3:割点和桥的求法
割点的充要条件:在搜索过程中,对于边(u, v),如果u为树根,则若u有两个以上的儿子节点,则u为割点;如果dfn[u]<= low[v],则u为割点。(后来的程序里貌似直接在v未访问过的情况下判断dfn[u]<= low[v])
桥的充要条件:对于边(u, v), 如果dfn[u] < low[v], 则(u,v)为桥(为什么不取’=’,见上面点边双连通所举得例子)。
可以在一个程序中同时求割点和桥:
stack<int> s;
void tarjan(int x, int fa)
{
dfn[x] = low[x] = time++;
s.push(x);
for(int e = first[x]; e != -1; e = next[e])
{
if(dfn[v[e]] == 0)
{
tarjan(v[e], x);
if(low[x] > low[v[e]]) low[x] = low[v[e]];
else if(dfn[x] < low[v[e]])
{
//说明边e是桥
}
}
else if(v[e] != fa)
{
if(low[x] > dfn[v[e]]) low[x] = dfn[v[e]];
}
}
//在对该节点访问之后判断x是否为割点,如果要求出强联通则
//需要在循环内判断
if(dfn[x] == low[x])//u是根
{
//u 是割点 <=> u 有至少两个子节点
}
else //x 是割点 <=> x 有一个子节点v[e],满足d[x]<= low[v[e]]
}
4:点双连通和边双连通
点双连通是在求割点的过程中把双连通分支求出来,每次将树边和反向边加入到栈中,如果遇到节点u存在节点v,使 dfn[u]<= low[v], 则找到一割点u,这时将边出栈,知道(u,v)出栈,得到的就是一个点双连通分支。由于无向图只存在树边和反向边,在循环的判断中可以通过这两这种边的特性来去除无向边的重复。树边表示v节点没有被访问,则dfn[v] == 0,即有dfn[v] < dfn[u];反向边也有dfn[v]< dfn[u]。所以用if(v != fa&& dfn[v] < dfn[u])可以将反向连接父亲的边,树边的反边,和反向边的反边(后两个是dfn[u] > dfn[v])。
stack<int> s;
int num = 1;
int time = 0;
int id[1000] = {0};
void tarjan(int x, int fa)
{
dfn[x] = low[x] = time++;
for(int e = first[x]; e != -1; e = next[e])
{
if(x != fa && dfn[x] < dfn[v[e]])
{
s.push(e);
if(dfn[x] == 0)
{
tarjan(v[e], x);
if(low[v[e]] < low[x]) low[x] = low[v[e]];
if(low[v[e]] >= dfn[x])//x是割点
{
int edge;
do{
s.pop();
edge = s.top();
id[u[edge]] = id[v[edge]] = num++;
}while(u[edge] != x || v[edge] != v[e]);
}
}
else if(dfn[v[e]] < low[x]) low[x] = dfn[v[e]];//只剩下反向边了
}
}
}
边双连通也是一样的过程,找到桥之后不断出栈。要注意的是桥的个数要比双连通数少1,最后节点无法全部出栈,借鉴网友的将num =1开始,id[]置为0,则最后剩下的点被自然分成一个标号为0的双连通分量了。
void tarjan(int u,int fa)
{
int e;
dfn[u]=low[u]=++time;
s[top++]=u;
for(e=first[u];e!=-1;e=next[e])
if(v[e]!=fa)
{
if(!dfn[v[e]])
{
tarjan(v[e],u);
if(low[v[e]]<low[u])
low[u]=low[v[e]];
else if(low[v[e]]>dfn[u])
{
for(s[top]=-1;s[top]!=v[e];)
id[s[--top]]=num;
num++;
}
}
else if(dfn[v[e]]<low[u])
low[u]=dfn[v[e]];
}
}
 爱华网
爱华网