本文除红色字体内容外,均来自网络。
假设检验是抽样推断的一个重要内容。所谓假设检验,就是事先对总体参数或总体分布形式做出一个假设,然后利用样本信息来判断原假设是否合理,即判断样本信息与原假设是否有显著差异,从而决定应接受式拒绝原假设。比如,对于某机器设备,生产工艺改变后,要检验新工艺对产品的某个主要指标是否有影响时,就需要抽样检验总体的某个参数(如均值、方差等)是否等于改变工艺前的参数值,这类问题就属于假设检验问题。
假设检验可分为两类,一是参数假设检验;二是非参数检验或自由分布检验,主要是总体分布形式的假设检验。本书只讨论几种重要的参数检验。
一、假设检验一般问题
(一) 假设检验的基本思想
先通过一个例子来说明假设检验的基本思想。
例6–16某企业生产一种零件,过去的大量资料表明,零件的平均长度为4厘米,标准差为0.1厘米。改革工艺后,抽查了100个零件,测得样本平均长度为3.94厘米。现问:工艺改革前后零件的长度是否发生了显著的变化?
这是关于工艺改革前后零件的平均长度(总体平均数)是否等于4的假设检验问题。我们知道,样本平均长度与原平均长度出现差异不外乎两种可能:一是改革后的总体平均长度不变,但由于抽样的随机性使样本平均数与总体平均数之间存在抽样误差;二是由于工艺条件的变化,使总体平均数发生了显著的变化。因此可以这样推断:如果样本平均数与总体平均数之间的差异不大,未超出抽样误差范围,则认为总体平均数不变;反之,如果样本平均数与总体平均数之间的差异超出了抽样误差范围,则认为总体平均数发生了显著的变化。
由上面例子可以看出,假设检验是对调查人员所关心的却又是未知的总体参数先做出假设,然后抽取样本,利用样本提供的信息对假设的正确性进行判断的过程。
(二) 假设检验的步骤
1.提出原假设和备择假设
对每个假设检验问题,一般可同时提出两个相反的假设:原假设和备择假设。原假设又称零假设,是正待检验的假设,记为H0;备择假设是拒绝原假设后可供选择的假设,记为H1。原假设和备择假设是相互对立的,检验结果二者必取其一。接受H0则必须拒绝H1;反之,拒绝H0则必须接受H1。
原假设和备择假设不是随意提出的,应根据所检验问题的具体背景而定。常常是采取“不轻易拒绝原假设”的原则,即把没有充分理由不能轻易否定的命题作为原假设,而相应地把没有足够把握就不能轻易肯定的命题作为备择假设。
一般地,假设有三种形式:
(1)H0:μ=μ0;H1:μ≠μ0。这种形式的假设检验称为双侧检验。如例6–14中可提出假设:H0:μ=4厘米;H1:μ≠4厘米。
(2)H0:μ=μ0;H1:μ<μ0(或H0:μ≥μ0;H1:μ<μ0)。这种形式的假设检验称为左侧检验。
(3)H0:μ=μ0;H1:μ>μ0(或H0:μ≤μ0;H1:μ>μ0)。这种形式的假设检验称为右侧检验。
左侧检验和右侧检验统称为单侧检验。采用哪种假设,要根据所研究的实际问题而定。如果对所研究问题只需判断有无显著差异或要求同时注意总体参数偏大或偏小的情况,则采用双侧检验。如果所关心的是总体参数是否比某个值偏大(或偏小),则宜采用单侧检验。在例6–14中,如果我们在乎的是零件长度是否比原来有所缩短,则可采用单侧检验,即H0:μ=4厘米(或μ≥4厘米);H1:μ<4厘米。
2.选择适当的统计量,并确定其分布形式
在参数的假设检验中,如同在参数估计中一样,要借助于样本统计量进行统计推断。用于假设检验问题的统计量称为检验统计量。在具体问题里,选择什么统计量作为检验统计量,需要考虑的因素与参数估计相同。例如,用于进行检验的样本是大样本还是小样本,总体方差已知还是未知,等等。在不同的条件下应选择不同的检验统计量。
3.选择显著性水平α,确定临界值
显著性水平表示H0为真时拒绝H1的概率。假设检验是围绕对水平假设内容的审定而展开的。如果原假设正确我们接受了(同时也就拒绝了替换假设),或原假设错误我们拒绝了(同时也就接受了替换假设),这表明我们做出了正确的决定。但是,由于假设检验是根据样本提供的信息进行推断的,也就有犯错误的可能。有这样一种情况,原假设正确,而我们却把它当成错误的加以拒绝。犯这种错误的概率用α表示,统计上把α称为假设检验中的显著性水平(Significantlevel),也就是决策中所面临的风险。所以,显著性水平是指当原假设为正确时人们却把它拒绝了的概率或风险。这个概率是由人们确定的,通常取α=0.05或α=0.01,这表明,当做出接受原假设的决定时,其正确的可能性(概率)为95%或99%。即拒绝原假设所冒的风险,用α表示。假设检验应用小概率事件实际极少发生的原理,这里的小概率就是指α。给定了显著性水平α,就可由有关的概率分布表查得临界值,从而确定H0的接受区域和拒绝区域。临界值就是接受区域和拒绝区域的分界点。
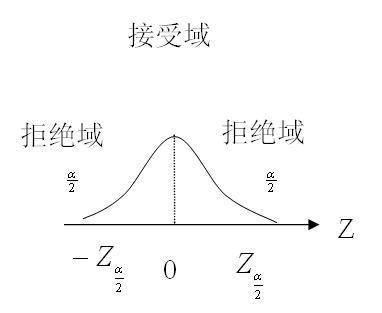
对于不同形式的假设,H0的接受区域和拒绝区域也有所不同。双侧检验的拒绝区域位于统计量分布曲线的两侧;左侧检验的拒绝区域位于统计量分布曲线的左侧;右侧检验的拒绝区域位于统计量分布曲线的右侧。如图6–2所示。
图6–2 假设检验的接受区域和拒绝区域
4.做出结论
根据样本资料计算出检验统计量的具体值,并用以与临界值比较,做出接受或拒绝原假设H0的结论。如果检验统计量的值落在拒绝区域内,说明样本所描述的情况与原假设有显著性差异,应拒绝原假设;反之,则接受原假设。
(三) 假设检验的小概率原理
假设检验的基本思想是应用小概率的原理。所谓小概率原理,是指发生概率很小的随机事件在一次实验中是几乎不可能发生的。根据这一原理,可以做出是否接受原假设的决定。例如,有一个厂商声称其产品的合格率很高,可以达到99%,那么从一批产品(如100件)中随机抽取1件,这一件恰好是次品的概率就非常小,只有1%。如果厂商的宣称是真的,随机抽取1件是次品的情况就几乎是不可能发生的。但如果这种情况确实发 生了,我们就有理由怀疑原来的假设,即产品中只有1%次品的假设是否成立,这时就可以推翻原来的假设,可以做出厂商的宣称是假的这样一个推断。我们进行推断的依据就是小概率原理。当然,推断也可能会犯错误,即这100件产品中确实只有1件是次品,而恰好在一次抽取中被抽到了。所以这个例子中犯这种错误的概率是1%,也就是说我们在冒1%的风险做出厂商宣称是假的这样一个推断。由此也可以看出,这里的1%正是前面所说的显著性水平。
二、总体均值、比例的假设检验
(一)总体方差已知时对正态总体均值的假设检验
设总体X~N(μ,σ2),总体方差σ2为已知,(x1,x2,…,xn)为总体的一个样本,样本平均数为。现在的问题是对总体均值μ进行假设检验。H0: μ=μ0(或μ≤μ0 、μ≥μ0 )。
根据抽样分布定理,样本平均数服从N(μ,σ2 /n),所以,如果H0成立时,检验统计量U 及其分布为:
利用服从正态分布的统计量U进行的假设检验称为U检验法。根据已知的总体方差、样本容量n和样本平均数,计算出检验统计量U的值。对于给定的检验水平,查正态分布表可得临界值,将所计算的U值与临界值比较,便可做出检验结论。
例6–17根据过去大量资料,某厂生产的产品的使用寿命服从正态分布N(1020,1002)。现从最近生产的一批产品中随机抽取16件,测得样本平均寿命为1080小时。试在0.05的显著性水平下判断这批产品的使用寿命是否有显著提高?
解:根据题意,提出假设:H0: μ=1020;H1:μ>1020,
检验统计量
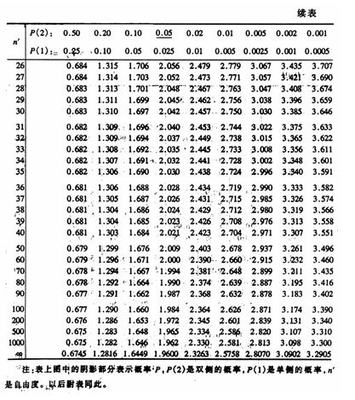
由α=0.05,查表得临界值U0.05=1.645
由于U=2.4>Uα=1.645,所以应拒绝H0而接受H1,即这批产品的使用寿命确有显著提高。
(二)总体方差未知时对正态总体均值的假设检验
设总体X~N(μ,2),但总体方差2未知,此时对总体均值的检验不能用上述U检验法,因为此时的检验统计量U中包含了未知参数。为了得到一个不含未知参数的检验统计量,很自然会用总体方差的无偏估计量–––样本方差S2来代替2,于是得到T统计量。根据上节内容已知道,检验统计量T及其分布为:
T
利用服从t分布的统计量去检验总体均值的方法称为T检验法。其具体做法是:根据题意提出假设(与U检验法中的假设形式相同);构造检验统计量T并根据样本信息计算其具体值;对于给定的检验水平α,由t分布表查得临界值;将所计算的t值与临界值比较,做出检验结论。
双侧检验时,若>tα/2,则拒绝H0,接受H1。
左侧检验时,若T< –tα,则拒绝H0,接受H1。
右侧检验时,若T>tα,则拒绝H0,接受H1。
例6–18从长期的资料可知,某厂生产的某种电子原件服从均值为200小时,标准差未知的正态分布。通过改变部分生产工艺后,抽得10件做样本得数据(小时):
202,209,213,198,206,210,195,208,200,207
解:根据题意,检验目的是考察电子原件的平均值数据是否有所提高。因此,可建立如下假设:
根据已知数据求得=204.8, S=5.789
检验统计量 T
由α=0.05,查表得临界值
注:在Excel中有两个t检验相关函数TTEST和TINV。如果想比较两列数据的差异,可以使用这两个函数。但是如果数据已经是平均值,而非原始数据,那么TTEST函数就没有用武之地了。利用TINV函数可以计算临界值,它有两个参数,概率和自由度。上题中概率为0.05;自由度为9(10-1),应该返回2.262。原作者数据1.8331系笔误,应该查t0.025,自由度为9的临界值。
由于,所以拒绝H0接受H1,即可以接受“在新工艺下,这种电子元件的平均值有所提高的假设”。
T检验法适用于小样本情况下总体方差未知时对正态总体均值的假设检验。随着样本容量n的增大,t分布趋近于标准正态分布。所以大样本情况下(n>30),总体方差未知时对正态总体均值的假设检验通常近似采用U检验法。同理,大样本情况下非正态总体均值的检验也可用U检验法。因为,根据大样本的抽样分布定理,总体分布形式不明或为非正态总体时,样本平均数趋近于正态分布。这时,检验统计量U中的总体标准差用样本标准差S来代替。
(三)总体比例的假设检验
由比例的抽样分布定理可知,样本比例服从二项分布,因此可由二项分布来确定对总体比例进行假设检验的临界值,但其计算往往十分繁琐。大样本情况下,二项分布近似服从正态分布。因此,对总体比例的检验通常是在大样本条件下进行的,根据正态分布来近似确定临界值,即采用U检验法。其检验步骤与均值检验时的步骤相同,只是检验统计量不同。
首先提出待检验的假设:
检验统量为
例6–19调查人员在调查某企业的主要生产线时,被告知性能良好生产稳定,产品合格率可达99%。随机抽查了200件产品,其中195件产品合格,判断厂方的宣称是否可信?(α=10%)。
解:依题意,可建立如下假设:
样本比例
由于样本容量相当大,所以可近似采用U检验法。
给定α=0.1,查正态分布表得
由于,应接受原假设,即认为厂方的宣称是可信的。
 爱华网
爱华网