常见的区分是
==========================
theta 表示 角度;
sigma 表示 正态分布中的 方差(注意 ),经常用样本方差 估算总体方差;epsilon对数的基数 以及误差项
deta表示 变分 ;
在积分中间: 大写gamma表示 曲线,大写sigma表示 曲面
拉普拉斯算法(正三角) 读法是 delta ,而 哈密顿算符 则是倒三角,读法是 naplanablasymbol:▽
-----------------------------------------------------------------------------
Laplace算符是正三角,或者是“▽”这个算符右上角加上一个二次方的标记,即“▽^2”。
“▽”这个算符叫做哈密顿算符,也叫劈尖算符,不同的情况下表示不同的意义,一般三种情况,读法也比太一样:
1,▽φ;读作“gradφ”,此时φ必须是个标势函数或标量,▽φ表示φ的梯度。
2,▽·A;读作“divA”,此时A必须是矢势函数或矢量,▽·A标势A的散度。
3,▽×A,读作“rotA”,此时A必须是矢势函数,或矢量,▽×A标势A的旋度。
一般来说,哈密顿算符只有上述四种用法,当然某些时候,为了形式简便,也会将Laplace算符(▽^2)与对时间的二阶偏导结合成d'Alembert算符,一般四维空间下它用的比较多。
------------------------------------------------------------------------------------------------------------
源自:http://tieba.baidu.com/f?kz=471801861
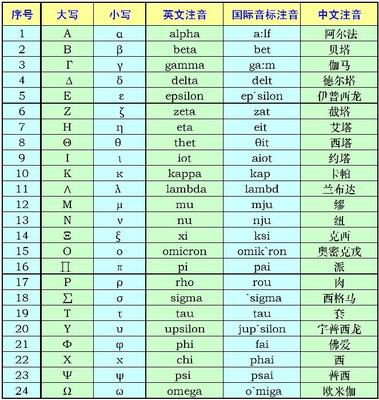
音标读法:
==========================
Α α alpha 角度;系数
Β β beta 磁通系数;角度;系数
Γ γ gamma 电导系数(小写)
Δ δ delta 变动;密度;屈光度
Ε ε,e epsilon 对数之基数
Ζ ζ zeta 系数;方位角;阻抗;相对粘度;原子序数
Η η eta 磁滞系数;效率(小写)
Θ θ,θ theta 温度;相位角
∏ π pi 圆周÷直径=3.1416
Ρ ρ,ρ rho 电阻系数(小写)
∑ σ,s sigma 总和(大写),表面密度;跨导(小写)
Φ φ phi 磁通;角
Ψ ψ psi 角速;介质电通量(静电力线);角
Ω ω omega 欧姆(大写);角速(小写);角
==========================
中文拼音读法
==========================
A α 阿尔法
B β 贝塔
Γ γ 伽玛
Δ δ 德尔塔
Ε ε 伊普西隆
Ζ ζ 泽塔
Η η 伊塔
Θ θ 西塔
Ι ι 约塔
Κ κ 卡帕
∧ λ 兰姆达
Μ μ 米欧
Ν ν 纽
Ξ ξ 克西
Ο ο 欧米克隆
∏ π 派
Ρ ρ 柔
∑ σ 西格玛
Τ τ 陶
Υ υ 玉普西隆
Φ φ 弗爱
Χ χ 凯
Ψ ψ 普赛
Ω ω 奥米伽
 爱华网
爱华网



