%%%%%%%%%%
%%方差分析
%%%%%%%%%
%作者:RUAN
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% %%%%%%%%%%%%%%%
%1.事情的发生往往与多个因素有关,但各个因素对事件发生的影响可能是不一样的,而且同一因素的不同水平对事件发生的影响也是不同的;
%2.通过发差分析,便可以研究不同因素以及因素的不同水平对事件发生的影响程度;
%3.根据自变量个数的不同,可分为单因子方差分析和多因子方差分析。
%注意:ANOVA函数的适用条件,所有样本数据:1)正态分布;2)具有相等的方差;3)观测量相互独立。
%%%%%%%%%%%%%%%
%%单因子方差分析
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%1.一项试验有多个影响因素,如果只有一个在发生变化,则称为单因子分析;
%2.基本原理:1)某一试验s个条件(或水平)下得到s个总体(X1,X2,...,Xs),平均数分别为(μ1,μ2,...,μs),方差分别为(σ21,σ22,...σ2s);
%2)在这个s个总体服从正态分布且方差相等的情况下,检验各总体的平均数是否相等,即检验假设H0:μ1=μ2=…=μs;
%3)当零假设成立时,认为因素对试验结果之间没有显著影响。
%离差平方和(SS):观察值与总平均值之差的平方和,——组间平方和(SSA)和组内平方和(SSE);
%总自由度(df=n-1),——组间自由度(dfA=s-1)和组内自由度(dfE=n-s);
%组间均方(MSA)和组内均方(MSE);
%当假设成立时,F=MSA/MSE=(SSA/dfA)/(SSE/dfE)服从第1自由度为组间自由度,第2自由度为组内自由度的F分布;一般应有F≈1;
%如果F值比1大得多,即条件误差比试验误差大得多,则条件(水平)不同起显著作用,因此,不能认为各总体的均值相同,故否定原假设;
%当F值小于1时,认为因素改变对试验结果引起的变动不显著,大部分试验误差由个体差异引起。
%F的大小反应了因子的各个水平不同引起的差异对随机因素作用引起的波动所占的比重,比值越大,说明由于因子的各个水平不同引起的差异越显著,即因子的各个水平的影响效应越显著。
%%函数anova1
p=anova1(X)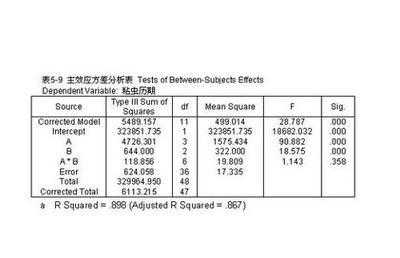
%比较样本m*n的矩阵X中的两列或多列数据的均值;其中每一列表示一个具有m个相互独立观测量的独立样本,它返回X中所有样本取自同一总体(或取自均值相等的不同总体)的零假设成立的概率p。若p值接近0,则认为零假设可疑,并认为至少有一个样本均值与其他样本均值存在显著差异。
%当p<0.05或0.01时,认为结果是显著的。(p是从F的累加分布函数(cdf)得到的,F增大时p值减小)
%anova1函数还生成两个图形(标准方差分析表和箱形图);
%%标准方差分析表(one-way ANOVA Table):
%1)由于列均值的差异导致的误差(组间差-group);2)由于每一列数据与该列数据均值的差异导致的误差(组内差-Error);3)总偏差-Total
%表中6列分别显示:1)偏差来源Source;2)SS(sums of squares);3)df(degrees offreedom);4)MS(mean squares);5)F;6)p。
%%箱形图
%箱形图中心线上的较大差异对应于较大的F值和较小的p值。
p=anova1(X,group)
%当X为矩阵时,用group参数(字符数组或单元数组)中的值作为X中样本的箱形图的标签。参数group中的每一行包含X中对应列中数据的标签,所以group的长度必须等于X的列数;
%不必按顺序对样本进行标注;
%若group中的一行包含i个空单元或空字符串,则该行和X中的对应观测量被忽视;
%anova1函数的矢量输入形式不需要每个样本中的观测量个数相同,它适用于不平衡数据。
p=anova1(X,group,'displayopt')
p=anova1(X,group,'off')
%当'displayopt'参数设置为'on'(默认设置)时,激活ANOVA表和箱形图的显示;'off'时不显示;
[p,table,stats]=anova1(X,group)
c=multcompare(stats)
stats
%1.返回ANOVA table;
%2.返回stats结构,用于进行多元比较检验。适用multcompare函数可以检验哪对均值差异显著,哪对差异不显著。
%3.c
%第1列为要比较的因素水平;
%第4列为被检验的2个因素水平的平均值的差的估计值;
%第3、5列为被检验的2个因素水平的平均值的差的95%置信区间。若置信区间包括0.0,则被检验的2个因素水平的均值差在0.05置信水平上不是显著的;否则是显著的。
%4.stats
%gname:因素水平的名称;
%n:3个因素水平的数据点数;
%source:结构statsnict031的来源;
%means:3个因素水平的数据的平均值;
�:组内偏差平方和的自由度;
%s:组内偏差的标准差。
%%%%%%%%%%%%%%%
%%双因子方差分析
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%当有多个因素同时影响试验结果时,采用多因子方差分析。因素即变量,变量的不同取值或者说因素的不同等级——因素水平;
%因素水平的改变所造成的试验结果的改变——主效应;
%当某一因素的效应随另一因素的水平不同而不同时,则称这两个因素之间存在——交互作用;
%由于交互作用引起的试验结果的改变称为——交互效应。
%【没有交互作用】SS=SSA+SSB+SSE[SSE:误差平方和;df:a-1,b-1,n-1-b+1]
%【存在交互作用】SS=SSA+SSB+SS(A*B)+SSE[SS(A*B):交互效应对应的离差平方和;df:a-1,b-1,(a-1)*(b-1),n-ab]
%%函数anova2
p=anova2(X,reps)
%进行平衡双因子方差分析,以比较样本X中两列或两列以上和两行或两行以上数据的均值。参数reps指示每个'单元'中观测量的个数。
%reps=1 [x11,x12;x21,x22;x31,x32;,x41,x42;...] 默认值
%reps=2 [x111,x111;x112,x121;x211,x122;...]
p=anova2(X,group,'displayopt')
[p,table]=anova2(X,group)
[p,table,stats]=anova2(X,reps,group)
c=multcompare(stats)
stats
%结果输出3个p值:[p1,p2,p3]
%p1:因子A存在主效应与否;
%p2:因子B存在主效应与否;
%p3:A,B是否存在交互效应。
%%%%%%%%%%%%%%%
%%多因子方差分析
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%anovan函数
%进行N因素方差分析
p=anovan(X,group)
%进行平衡或不平衡数据的多因子方差分析,比较矢量X中的观测量相对于N个不同因子的均值;
[p,table,stats,terms]=anovan(...)
%返回方差分析计算中用到的主项和交互项;项目用与输入参数'model'相同的格式编码到输出矩阵terms中。
[p,table,stats,terms]=anovan(X,group,'displayopt',on,'model',modeltype)
%modeltype可以是linear,interaction,full;
%'linear'模型为默认选项,只计算N个主效应零假设的p值;
%'interaction'模型计算N个主效应和(N,2)二因子交互效应零假设的p值;
%'full'模型计算N个主效应和所有水平交互效应零假设的p值;
%整数k(k≤N):anovan函数计算所有水平与第k水平交互效应零假设的p值。例如k=3,表示主效应加上2因子和3因子交互效应。k=1等价于‘linear’;k=2等价于‘interaction’;k=N等价于‘full’。
%矩阵:[0 01]主项A;[0 1 0]主项B;[1 0 0];主项C;[0 1 1]交互AB;[1 1 0]交互BC;[1 0 1]交互AC;[11 1]交互ABC。矩阵用来设置modeltype
[p,table,stats,terms]=anovan(X,group,'model',[0 1 0;0 0 1;0 11])
%输出矢量p包含主效应B,C和交互效应BC的零假设的p值。
p=anovan(X,group,'model',integer)
%用integer指定的平方和类型进行方差分析,integer可以取1,2或3,分别指定第1种、第2种或第3中平方和。默认值为3.integer的值只影响非平衡数据的计算。
%%%%%%%%%%%%%
%%方差分析工具
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%用aoctool函数生成进行方差分析模型拟合和预测的交互图。
aoctool(x,y,g)
%用g数组中的值对列矢量x和y中的值进行分组,然后分别用直线进行拟合。输出包括数据和预测曲线的交互图、方差分析表和参数估计表。
aoctool(x,y,g,alpha)
%确定预测区间的置信水平。置信水平为100*(1-alpha)%,alpha的默认值为0.05。
aoctool(X,y,g,alpha,xname,yname,gname)
%指定图中或表中x,y,g参数的名称。
aoctool(X,y,g,alpha,xname,yname,gname,'displayopt')
%激活或取消图形和表格的显示。
aoctool(X,y,g,alpha,xname,yname,gname,'displayopt','model')
%指定进行拟合的初始模型。
%'model'的值可以选择:
%'samemean'忽略分组,拟合单个均值;
%'separatemeans' 对每个组拟合均值;
%'sameline'忽略分组,拟合单条直线;
%'parallellines'为每个组拟合单条直线,但要求直线必须平行;
%'seperatelines' 为每个组拟合单条直线,没有约束。
h=aoctool(...)
%返回图中直线对象的句柄矢量。
[h,atab,ctab]=aoctool(...)
%返回包含方差分析表(atab)和系数估计表(ctab)中入口的单元数组。
[h,atab,ctab,stats]=aoctool(...)
%返回一个stats结构,以进行多重比较检验。
c=multcompare(stats)
stats
 爱华网
爱华网