判别分析是经典的分类预测方法,它根据已有的训练样本,确定分类型输出变量与数值型输入变量之间的数量关系,其使用的中介,是判别函数。
判别分析非常常见,本博尝试从Clementine、Spss和R三个角度来切入判别分析。
判别分析的分类:
按输出的分类变量的数目分为两组判别分析和多组判别分析;根据所采用的数学模型,分为线性判别分析和非线性判别分析;根据判别准则,可以分为距离判别法、Fisherr判别法和Bayes判别法。这些都集中在Clementine的判别分析节点上。
8.2.1 距离判别法
设某样本可分为K组(即输出的分类变量有K个类别),且每个样本都有P个变量(P>K),且输入型变量都为数值型变量,服从正态分布。距离判别法的思想是:将N个样本数据看做是P维空间中的点,则一个样本通过它的P个变量取值,就可以在P维空间中得到惟一位置。这样,计算出K个分组中每个组的各输入变量的均值,通过这P个均值的组合,在P维空间得到惟一点,称为此分组的类别中心。对于新数据,计算它到各类别中心的马氏距离,并根据距离最近的原则,新数据点距离哪个类别近则属于哪个类别。
判别分析的目的是得到相应的判别函数,从而得到能够将不同总体区分开的线、平面或超平面。需要注意的是,做判别分析要求不同变量的数值分布要呈正态分布,严格意义上讲,多元变量的分布也要呈多元正态分布,相关内容我们会在Spss的判别分析中介绍。除了正态性外,判别分析还要求不同类别的总体间有显著性差异,否则错判率会较高。
8.2.2Fisher判别法
Fisher判别分析的核心思想是先投影,再判别。Fisher判别法的判别函数是输入变量的线性函数形式,其中的系数我们称为判别系数,表示输入变量对于判别函数的影响。所谓投影,指将原来P维的X空间的输入变量组合投影到K(K<P)维的Y空间中去,实现了坐标系统的变换,坐标系统的变换原则是,尽可能把来自不同类别的样本区分开。
首先,应该在输入变量的P维空间中找到某个线性组合,使各类别的平均值差异最大,作为第一维 度,代表输入变量组间方差中的最大部分,得到第一判别函数。
然后,按照同样规则依次找到第二判别函数,第三判别函数等,且判别函数之间独立。
因此,我们通过Fisher判别法得到的判别函数代表了输入变量间的方差,一般第一判别函数代表的组间方差是最大的,所以我们往往会发现最后的判别分析图中,不同类别在第一维度即第一函数上的分布,是差异最大的。
则所有判别函数所代表的组间方差比例之和,为1。
在判别分析过程中,我们对判别函数的要求是,使组间方差越大越好,组内方差载小越好。
那么,应该取几个判别函数呢,一般有两个标准。第一,指定取特征值大于1的特征值;第二,前M个判别函数的判别能力达到指定的百分比。
对新数据的预测与距离判别法相似,通过判别函数计算出新数据在Y空间中的位置,然后计算其与各类别中心的距离,最近,则属于该类别。
8.2.3 Bayes判别法
Bayes差别法属于Bayes方法范畴,Bayes方法是一种研究不确定性的推理方法,其不确定性用Bayes概率表示。Bayes概率的估计取决于先验知识的正确性和后难知识的丰富性,其会随人掌握信息的不同而发生变化。如某部影片上映后获得理想票房的收入的概率,在未上映之前主要取决于电影发行商多年的经验,但在电影上映过程中此概率并定得到调整,增大或者减小。
关于Bayes,我们在这里不再多谈。
8.2.4 判别分析应用示例
导入Spss数据,此数据是一份关于MBA招生的数据,含三个变量:平均学分成绩、管理才能得分和录取结果。其中前两个输入变量为数值型变量,最后一个输出变量为分类变量,含有录取、不录取和待定三个水平。依次添加SpssFile和Type节点对数据进行读取和字段方向设置,添加Modeling中的Discriminate节点,设置相关参数。
在方法方面Clementine提供了两种方法,一是Enter,一是Stepwise。Enter是强制进入法,即所有输入变量都参加模型的构建;Stepwise为逐步筛选法,Stepwise法可以挑选出具有高判别能力的输入变量进入判别函数。
逐步筛选法与回归分析中的逐步回归法思想相似。即采用的是“有进有出”的策略,逐步引入最重要的输入变量,并随机判断是否有其它输入变量因为后续的操作而不再显著。如果有输入变量的判别作用下降,则将其剔除出去,直到所有输入变量进入,而不再有输入变量的作用低于显著性水平。通过,我们会用WilksLambda统计量为此函数的效果进行检验。
一、准备工作:均值检验和方差性次性检验
1、均值检验
我们知道,进行判别分析的一个条件是各类别间输入变量的均值具有显著性差异,为此我们要通过检验统计量WilkLambda进行检验人。此检验同方差检验,其统计量等于SSE/SST,即组内变差除以总变差,此统计量服从Wilks分布,也可以用卡方分布近似。
具体的操作是选择Expert面板,选择Expert,然后在“输出”中进行设置:
在输出面板中进行设置。选择描述性分析中的均值和单变量ANOVAS,表示显示各类别的变量均值并对其进行方差分析。
如下图,给出了各类别中不同输入变量的均值和方差,在后面显示了加权情况。第二张表显示的是对不同输入变量的均值检验,我们只看Sig列,发现两列都具有显著性,说明输入变量均值拥有显著性差异,则可以适用于判别分析。
2、方差齐次性检验
在距离判别法中,各总体的协方差矩阵相等和不相等时,采用的判别函数是不同的,因此我们在输出中选择BoxM进行方差齐次性检验。以显示了不同组内和组间的协方差矩阵和相关系数矩阵。显然三组协方差矩阵存在明显差异,在使用协方差矩阵的选项中,我们选择使用独立组。
二、解读判别结果
在输出面板中的Function Coefficients中选择未标准化项,显示未标准化的判别函数系数。
1、Fisher判别函数
下图给出了未标准化的Fisher判别系数,则根据未标准化的判别系数可以得同两个判别函数为:
Y1=-15.595+4.086X1+0.007X2
Y2=-1.47+-1.831X1+0.014X2
将原数据的相应值代入两个函数,可以得到样本点在Y空间的坐标。
下图给出了三个类别在该新空间中的坐标。注意,这是三个类别的中心在两个判别函数中的得分,可以根据两个得分画出其中心所在位置。
下图为标准化后的判别系数。标准化后的判别系数克服了原始数据中量纲差别造成的影响,反映的是不同输入变量对新样本坐标确定的贡献率。由图可知,大学平均成绩对第一坐标的贡献最大,管理才能评分对第二坐标的贡献率最大。
下面为结构矩阵,StructureMatrix。揭示了不同输入变量对判别函数的相关性,是简单相关系数修正后的结果。星号表示相应系数的绝对值最大,表明第一判别函数与大学平均成绩的相关性高,第二判别函数与管理才能的评分相关性高。
2、判别能力检验
那么,Fisher判别函数的投影是否很好地实现了各类样本分开的效果呢,哪个判别函数更重要?下图第一张显示了特征根,我们看到第一函数和第二函数的特征根,组间方差解释百分比,累积百分比和相关性。其中,特征根表征了判别函数携带信息的量,越大,表示携带组间方差越大。相关系数表征了判别函数与不同类别的相关性,其中相关性越大,表示不同类别在此维度上差异越明显。
第二张显示了WilksLambda,即从统计检验角度分析哪个判别函数表现出的判别能力是显著的。我们看到第一二判别函数综合起来的判别效果二判别函数的效果一样,都有显著性。
3、Fisher判别函数
在输出面板的函数系数中选择Fisher's,得到Fisher判别函数如下。费舍尔线性判别函数相关矩阵,利用此矩阵将新数据的值代入,哪个类别的结果值大,则属于哪个类别
4、各样本的详细判别结果
在Classification框中选择Casewise reults项表示显示前面若干个样本的详细判别结果。可在Limitcase to first框中指定想查看的样本个数,默认为前十个。如下所示,判别分析生成判别模型后,还会应用于自己原有的数据上进行验证。下图中预测组中带星号的表示预测错误,不带星号表示预测正确。“到质心的平方马氏距离”列表示此数据点距离该类别中心点的马氏距离;第二最高级中的“组”列是通过Bayes判别得出的第二高的判别结果,后面的P值为相应的贝叶斯概率。注意最右侧的两列得分,这是此点在第一判别维度和第地判别维度上的得分,通过这两个得分,我们就能和到此点在二维图像上的位置。
5、判别结果的评价
通过勾选Classification中的SummaryTable,得到判别分析的混淆矩阵。在混淆矩阵中,我们可以查看模型的预测能力。如下图示,在类别1中,模型成功预测30项,错判1项,成功率为0.968;类别2和类别3同理。注意,总体预测成功率为最底部的0.953,说明此模型相当不错了已经。
7、Plot
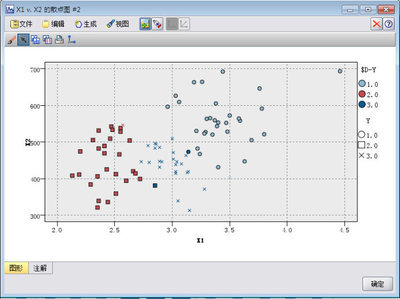
那么,我们能不能像对应分析那样将分类的模型展现在图中呢?添加Plot节点,并进行相关设置,得如下图。我们看到三个类别的点很明显地彼此区分了开来。
 爱华网
爱华网