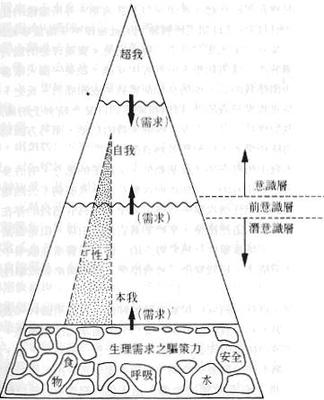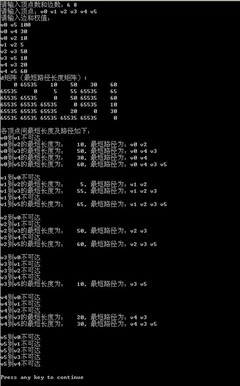
Floyd-Warshall算法(FloydWarshallalgorithm)是解决任意两点间的最短路径的一种算法,可以正确处理带权有向图或负权的最短路径问题 解决此问题有两种方法: 两种算法的时间复杂度均为O(n3),但后者形式上比较简单。 |
(3)依次向S中加入v0 ,v1…vn-1,每加入一个顶点,对dist[i][j]进行一次修正:设S={v0,v1… vk-1},加入vk,则dist(k)[i][j] = min{dist(k-1)[i][j],dist(k-1)[i][k]+dist(k-1)[k][j]}。
dist(k)[i][j]的含义:允许中间顶点的序号最大为k时从vi到vj的最短路径长度。
dist(n-1)[i][j]就是vi到vj的最短路径长度。
最短距离有三种情况:
1、两点的直达距离最短。(如下图)
2、两点间只通过一个中间点而距离最短。(图)
3、两点间用通过两各以上的顶点而距离最短。(图)
对于第一种情况:
在初始化的时候就已经找出来了且以后也不会更改到。
对于第二种情况:
弗洛伊德算法的基本操作就是对于每一对顶点,遍历所有其它顶点,看看可否通过这一个顶点让这对顶点距离更短
对于第三种情况:
如下图的五边形,可先找一点(比如x,使=2),就变成了四边形问题,再找一点(比如y,使=2) ,可变成三角形问题了(v,u,w),也就变成第二种情况了,由此对于n边形也可以一步步转化成四边形三角形问题。(这里面不用担心哪个点要先找哪个点要后找,因为找了任一个点都可以使其变成(n-1)边形的问题)。
Java代码
 爱华网
爱华网