——由福建统计年鉴2012提供的数据计算基尼系数的详解——
在我的上一篇《洛仑兹曲线与基尼系数的实例诠释——由上海统计年鉴2012提供的数据诠释洛仑兹曲线和基尼系数的概念》中,以上海统计年鉴2012提供的数据介绍了洛仑兹曲线和基尼系数的基本概念。即:反映了收入分配均衡的基尼系数是洛仑兹曲线的积分面积比例,但对基尼系数计算的细节并未探讨。本文利用福建统计年鉴2012提供的相关数据,进行适当整理后,使用Excel中提供的的散点图来绘制洛仑兹曲线;用Excel散点图中添置趋势线方式自动拟合方程,来模拟解决洛仑兹曲线方程;用定积分来求解模拟的洛仑兹曲线下面积;最后使用基本的四则运算求得基尼系数。
⒈数据调整和处理
由下列网址可查阅到《福建统计年鉴-2012》”的第七篇“人民生活”表7-5:按人均可支配收入分组的城镇居民家庭基本情况(2011年)如表-1所示,此次调查按户为基本统计单位,并按其收入水平分为“最低收入”“低收入”、“中等偏下收入”、“中等收入”、“中等偏上收入”、“高收入”和“最高收入”七组,各组占调查总户数的比重(%)也已标注:
(年鉴:http://www.stats-sh.gov.cn/tjnj/nj12.htm?d1=2012tjnj/C0912.htm
表格:http://www.stats-fj.gov.cn/tongjinianjian/dz2012/index-cn.htm)
表-1
我们将上述表-1中与“家庭总收入”相关的红色矩形框出的数据单独列出。又因为我们关心的是其中个各类别家庭收入占所有家庭收入总和的比率,所以增加单元格AB40置入对U40:AA40求和公式作为总计,并为了计算各组所占总体的比率,增加一行“各组类别家庭总收入占所有家庭收入总计的比率(%)”由T41:AA41中公式可见(此处对求和单元格$AB$40为绝对引用);再由低到高逐组对百分比做累加,如表-2中T39:AA39;T42:AA42两行公式所示
表2
对表-2视图显示方式取消“公式”的勾选,则显示出各单元格的数字显示,如表-3所示:
表-3
⒉插入带平滑线的散点图
选取单元格区间T42:AA42,插入带平滑线的XY散点图的图表,在“源数据”中选取T39:AA39为x轴标志,以S36为系列标题名称,如图-1所示:
图-1(上:2003版下:2010版)
确定后,调整坐标轴、取消图例,完成后得到图2所示带平滑线XY散点图,该曲线就是洛仑兹曲线。根据统计数据绘出的数据点都是一些离散的点,平滑地连接起来是一条不规则的曲线,并没有确定的方程,为了取得这条曲线的拟合方程,需做后续处理。
图-2
⒊添加趋势线,取得模拟曲线方程
如图-3所示,右键点击曲线,在弹出的右键菜单上选择“添加趋势线”:
图-3(上:2003版下:2010版)
在弹出的【添加趋势线】对话框中,切换到“类型”选项卡,在“趋势预测/回归分析类型”中,方程的类型和次数可视拟合程度调整,不过选择多项式的话,在之后的使用积分求原函数的公式比较方便,本例根据原曲线走向趋势及考虑后续的积分求原函数计算方便,选择“多项式”,在“阶数”上下箭头调整选择上先可调节为2,视曲线与点拟合程度还可调整为3、4、5、6等。如图-4所示:
图-4(上:2003版下:2010版)
切换到“选项”选项卡,选中“设置截距= 0”、“显示公式”和“显示R平方值”复选框,如图-5所示:
图-5(本图为2003版。2010版已包含在图-4了)
确定后,可见原图中出现趋势线,即拟合曲线。在图-6中,如图示说明,二次曲线的拟合程度不够理想,模拟的绿色的二次曲线上的数据点离原始曲线较远,与原始曲线差异较大(R平方值只有0.9545);将图-4中多项式次数调正为3,再次取得的模拟的红色三次曲线与原始曲线较为接近,R平方值也达到0.9922,
图-6
由于我们下面要以三次曲线为例示意面积并计算,故单独将三次曲线与原曲线对比,如图-7所示:
图-7
⒋准备为绘制曲线面积图的数据表
为了直观形象地说明基尼系数是与洛仑兹曲线相关的面积比,以上述所得趋势线方程作为模拟的洛仑兹曲线方程来进行绘图,要准备相关的数据表。以下两张表其实是一张表的不同显示形式:表-4主要演示运算过程的公式,表-5所示为作图所需的全部表格的数据值。
如表-5所示:在单元格区域AF45:AP45设置自变量x的值,从0到1,相邻数据等差为0.1。因为方程的表达式为:
y=2.2719x^3-2.3008x^2+0.9991x,所以,在AF46中置入公式:
“=2.2719*AF45^3-2.3008*AF45^2+0.9991*AF45”,其中AF45的值是自变量x的值,为相对引用。将公式复制到AF46:AP46,如表-4所示:
表-4
将表-4显示形式取消“公式”勾选,恢复数值显示,如表-5所示:
表-5
⒌绘制与洛仑兹曲线相关的面积图
由于基尼系数是洛仑兹曲线的积分面积比例,必然要绘制与洛仑兹曲线相关的面积图。
我们用Excel图表中的面积图绘制洛仑兹曲线,先绘制绝对平均区域的对角线三角形面积图,并以某显著颜色图案着色。再绘制洛仑兹曲线,选择一个前景色着色,掩盖前者的一部分以后,就可见到月牙形的曲边形,从而为基尼系数的计算做了准备。
选择表-5中单元格AF46:AP47作图表,选择“面积图”第一行第一个“面积图。显示各种数值随时间或类别而变化的趋势线”,如图8所示:
图-8
在图-8中并未见到实际分配的拟合曲线面积图,这是由于面积图形系列的叠放次序需要调整。右键单击紫色面积,选取“数据系列格式”,在弹出的“数据系列格式”的选项卡中选取“系列次序”,选中“理想收入分配曲线y=x”,再点击“下移”,然后确定,如图-9所示:
图-9(上:2003版下:2010版)
这时洛仑兹曲线与绝对平均的分配曲线都显示出来了,如图-10所示:
图-10
⒍求基尼系数
由于洛伦兹曲线常用来形象化地说明问题,它不可能用一个确切的数字来表示收入差异的总体水平,国际通用的衡量这种水平的最常用的是基尼系数。基尼系数是从洛伦兹曲线推导出来的,用以测定洛伦兹曲线背离完全均等状况的程度。基尼系数是洛仑兹曲线的积分面积比例,基尼系数的计算是这样的:
设:洛伦兹曲线和对角线之间的那块月牙形区域(图中紫色区域)面积为S,
绝对不均等折线和绝对均等对角线围成的直角三角形OAB区域的面积为P,通常这个P是个定值0.5。
基尼系数G=S/P=月牙形区域(图中紫色区域)面积/SRt△OAB
其中,月牙形区域(图中紫色区域)面积=SRt△OAB—蓝色曲边形面积=0.5―蓝色曲边形面积
蓝色曲边形面积的求法就是关键,求得它,一切迎刃而解。
而蓝色曲边形面积就是洛仑兹曲线下面积,即曲线y=2.2719x3-2.3008x2+0.9991x下面积,这一曲边形面积的计算有很多专业的方法,这里不再一一赘述。不过尽管我们不是专业人员,但还是有一些办法可以解决这个问题的。回忆一下大学一年级学习的高等数学,为求曲线和坐标轴所夹曲边梯形的面积,可以通过将其分割成许许多多梯形,然后将这些梯形面积累加而成,而这种无限分割,然后无限积累的思想,就是微积分的基本思想,也就是说,这一数值是可以通过定积分求得。
于是,如果蓝色曲边形面积求得,那么,月牙形区域(图中紫色区域)面积也就可求得:
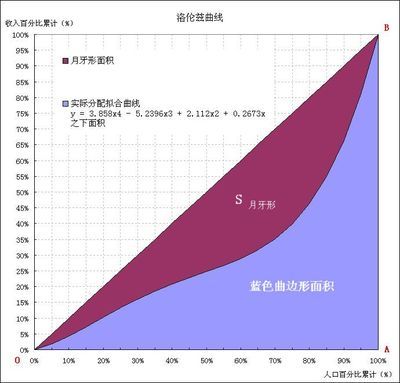
由此,算得本次基尼系数的值是G=0.398817
上述计算基于三次多项式模拟洛仑兹曲线,如果使用四次多项式模拟,如图-11所示。显然四次曲线(红色实线)与原始曲线(虚线)靠得更近,比三次曲线(黑色实线)拟合度更好一些,R平方值也从0.9922提高到0.9993:
图-11
以四次曲线方程y=3.858x4-5.2396x3+2.112x2+0.2673x绘制洛仑兹曲线下面积图如图-12所示(如仅仅计算基尼系数,该图不必作):
图-12
据此,计算基尼系数:
由四次曲线拟合洛仑兹曲线,求得基尼系数G=0.4023
可以继续测试。
以五次曲线拟合,求得曲线方程y=3.9258x5-5.8887x4+3.0891x3-0.6787x2+0.5538x,R平方值为0.9996,如图-13所示:
图-13
做成相应的面积图,如图-14所示(如仅仅计算基尼系数,该图不必作):
图-14
求得基尼系数 G=0.400997
以六次曲线拟合,求得曲线方程y = 0.5691x6 + 2.2217x5 - 3.9848x4 + 2.1179x3 -0.4602x2 + 0.5375x,R平方值为0.9996,如图-15所示:
图-15
做成相应的面积图,如图-16所示(如仅仅计算基尼系数,该图不必作):
图-16
求得基尼系数 G=0.401103
如果模拟曲线与实际收入曲线接近的程度越高,也就是方程的拟合程度越高,曲边形面积计算的误差越小,基尼系数也就也接近实际值。上述测试使用了无常数项的,截距为0的过原点的三次三项式、四次四项式、五次五项式和六次六项式的曲线来逐次逼近实际分配曲线,从而使测定的基尼系数逐次逼近某个值,比如这次测定的四个值在0.40左右摆动:
G(3次)=0.398817、G(4次)=0.4023、G(5次)=0.400997、G(6次)=0.401103
如果不是要求太高可以认为此次测定基尼系数为0.40.
据有关组织规定:若
收入的基尼系数<0.2表示收入分配绝对平均;
收入的基尼系数介于0.2~0.3表示比较平均;
收入的基尼系数介于0.3~0.4表示相对合理;
收入的基尼系数介于0.4~0.5表示收入差距较大;
收入的基尼系数>0.6以上表示收入分配差距悬殊。
据此,本次测定的基尼系数0.40处于分配相对合理的末端,开始进入收入差距较大的范畴。考虑到这是对福建省城镇居民的抽样,而福建省从沿海的福州、厦门到莆田、泉州再到离海较远的龙岩等,地域跨度、经济跨度较大,这一结果也反映了一定的实际情况。
根据上面的基本方法,可以了解求基尼系数的步骤如下:
⒈数据的整理和处理:将数据由低到高排列,均分为n组;求得各组人口与收入占总体的比率;逐组将百分比累加;
⒉插入带平滑线的XY散点图:在Excel中,以各组收入比率累加值为数据,以各组人口比率累加值为x轴单位插入XY散点图;
⒊添加趋势线,取得模拟的洛仑兹曲线方程:利用Excel散点图添加趋势线,自动取得趋势线及其方程,多次试验,采用拟合度较好的趋势线方程作为模拟的洛仑兹曲线方程;
⒋准备为绘制曲线面积图的数据表(如仅仅计算基尼系数,本步骤不必):根据上述确定的模拟的洛仑兹曲线方程的列出数据表;
⒌绘制与洛仑兹曲线相关的面积图(如仅仅计算基尼系数,本步骤不必):根据上述表格使用Excel中的面积图绘制洛仑兹曲线面积图(有时需调整系列次序以保证洛仑兹曲线下的面积显性显示);
⒍求基尼系数:对选定的洛仑兹曲线的模拟曲线方程使用定积分求得曲线下面积,再利用差、比的运算求得基尼系数。
【附录】我的博客中与洛伦兹曲线与基尼系数有关的文章及其链接地址:
《走下神坛的基尼系数——由上海统计年鉴2012提供的数据诠释洛仑兹曲线和基尼系数的概念》
http://shuchonghui.blog.163.com/blog/static/1511563201302344208/
http://blog.sina.com.cn/s/blog_a20c88b6010155m6.html
《使用Excel计算基尼系数的实例剖析——由福建统计年鉴2012提供的数据计算基尼系数的详解》
http://shuchonghui.blog.163.com/blog/static/1511563201302470918/
http://blog.sina.com.cn/s/blog_a20c88b6010155mf.html
《亚洲四国洛伦兹曲线对比的绘制实例》
http://shuchonghui.blog.163.com/blog/static/151156320130272851788/
http://blog.sina.com.cn/s/blog_a20c88b6010155mk.html
《基尼系数递减性及其图例解析》
http://shuchonghui.blog.163.com/blog/static/151156320130274054781/
http://blog.sina.com.cn/s/blog_a20c88b6010155mt.html
《用Excel表达贫富不均——洛仑兹曲线的绘制及基尼系数的定积分计算》:
http://shuchonghui.blog.163.com/blog/static/151156320095272211692/
《使用Excel计算曲线下面积》
http://shuchonghui.blog.163.com/blog/static/1511563200961295223931/
《答MZY:Excel指定区间的曲线下面积》
http://shuchonghui.blog.163.com/blog/static/1511563201162382330927/
 爱华网
爱华网