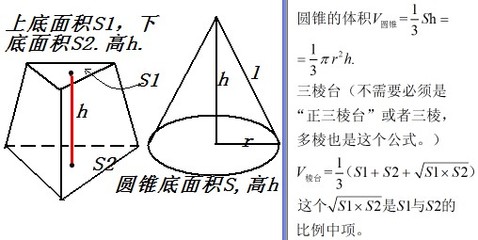
这一次我们带给大家的是有关于圆锥体积公式的得出。相信大家早在小学阶段就已经学过了圆锥体积 V=1/3sh,也就是底面积×高再除以3,大家有没有想过这是为什么呢?
首先,我先向大家说明一下思路:大家是否还记得圆的面积怎么求吗?对了,它用的是一种叫做“无限等分”的方法来得出一个近似的长方形。圆锥也可以把它看做是无数个同高不同底的圆柱叠加而成,然后作出一个无限近似的圆锥,如果有不了解的可以去图片那里看一看有关的图片。
好的,思路介绍 完了就要进入正轨了。首先,我们要说明一个定理:在一个直角三角形内1/x高(距离顶点)的地方的底是原底的1/x。
看一下圆锥的剖面,一个等腰的三角形,沿高切开就成了一个直角三角形,它的底就是圆锥的r,高就是圆锥的h;由上面的定理可以得出在圆锥距离顶点h/x处的r是r/x。也许会有人不了解为什么“在一个直角三角形内1/x高(距离顶点)的地方的底是原底的1/x”,我来解释一下——假设那个三角形的原底是a,在h/x的地方的底是b,那么根据勾股定理得出:h÷a=h/x÷b然后是b/a=1/x最后a/b=x所以a×(1/x)=b。
圆柱体积的公式是:πr²h圆锥的就是v={[(1/n)r]²(h/n)π}+{[(2/n)r]²(h/n)π......+{[(1/n)r]²(h/n)πn的值取决于你要把圆锥分成几份,当然,这个值当然越大越好。[(1/n)r]²可以化为(1/n)²×r²公式优化完之后就变成了[(1/n)²+(2/n)².....+(n/n)²]×r²×h/n×π也可以是 [1²+2²......+n²]×r²×h/n×π÷n²
在这里要说一下,假设我们要求1²+2²......+n²,那么这个得数就等于n×(n+1)×(2n+1)÷6。
这个公式是怎么得到的呢?在这里我做一个简单的说明:在大纸上画三个三角形,然后再顶点处标上1,下一行就是2个2,然后是3个3,一直到n个n,那么,这个三角形里面所有数字的总和就是这个连续平方的和,另一个三角形就把1标在左下角,然后右边就是2个2,第三个就把1标在右下角,以此类推。那么,你会发现,在三角形的同一个位置上三个不同的三角形在该位置上的数字为2n+1,那么有多少个2n+1呢?有n*(n+1)/2个,两个相乘再除以三九得到了:(2n+1)*(n+1)*n/6
最后得出来n×(n+1)×(2n+1)÷6×r²×h/n×π÷n²。
代入一下:n=100000 r=1 h=1π≈3.14100000×100001×200001÷6×1×0.000001×3.14÷10000000000=1.0466776566719用v=sh÷3得出约是1.046666666666667相差毫厘。
那么,为什么只是近似而不是正好是1/3呢?现在让我们进入极限的步骤:
n*(n+1)*(2n+1)=(n^2+n)*(2n+1)=2n^3+2n^2+n^2+n=2n^3+3n^2+n
然后再用lim(limit)n→∞(2n^3+3n^2+n)/6n^3=1/3n^3于是我们就得到了圆锥的体积公式!
现在让我们总结一下:我们是如何solve this problem的呢?首先我们先把它分成好多好多个小块,然后再求出每个小块之间的共同特征,然后再把它们垒在一起,复原这个图形,然后再取极限(limit),我们就得到了它(圆锥)的体积公式。我们的第一步切分图形,把圆锥切分成无限个小块然后求它们之间的关系便是一个微分的过程;然后我们再把它们加起来取极限,这就是积分的过程;而我们把一个整体(圆锥)分成无数份和后面的取极限就是微积分(calculus)里面的极限。那么,我们所做的这一切就是一个微积分的过程了。
 爱华网
爱华网


