[转自wiki]欧拉-拉格朗日方程对应于泛函的临界点。在寻找函数的极大和极小值时,在一个解附近的微小变化的分析给出一阶的一个近似。但是它并不能分辨是找到了最大值或者最小值或者两者都不是。在理想的情形下,函数的极大值及极小值会出现在其导数为0的地方,同样的,求解变分问题时也可以先求解相关的欧拉-拉格朗日方程。方程的具体形式:
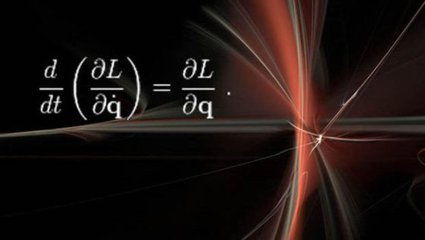
第一方程:
,使得泛函取得局部平稳值,则在区间內對於所有的,皆有:
第二方程:
设,及在中連續,若使得泛函取得局部平穩值,則存在一常數,使得:
注意,欧拉-拉格朗日方程式极值的必要条件,并非充分条件。
解释一下为什么可以使用变分法来求解能量极小的问题。这是由于,当能量函数包含微分时,可以用变分方法推导其证明过程。简单的说,证明思路是:假设当前的函数(即真实解)已知,那么这个解必然使能量函数取全局最小值。换言之,在此真实解上加入任何扰动,都会使能量函数变大。当扰动的能量趋于0时,能量函数关于扰动的导数就是0.关键问题是扰动如何 表示,才能便于上述过程的实现呢?答案就是扰动被表示成一个幅度很小的连续函数乘以一个扰动因子a,当a趋于0时意味着扰动的能量趋于0,这时能量泛函对a求导等于0就等价于能量泛函对扰动求导等于0。不得不承认这时一个非常绝妙的问题转化,把对函数的求导变为对单变量的求导。然后再利用变分算子的基本引理,就可以证明了
 爱华网
爱华网