转载 matlab分段函数绘图 matlab画分段函数图像

1.一元分段函数绘图

例如：

把下面的函数保存为Piecewise_x.m文件

functionF=Piecewise_x(x)
F=x.^2.*(x>=0 &x<1)+cos(pi*(x-1)).*(x>=1&x<2)+(-x.^2./(x+2)).*(x>=2& x<=4);
end

运行：

x=linspace(0,4);
F=Piecewise_x(x);%计算相应函数值
plot(x,F);%绘制曲线
hold on;
plot(1*ones(1,2),ylim,'r:');%画区间间隔线
plot(2*ones(1,2),ylim,'r:');%画区间间隔线

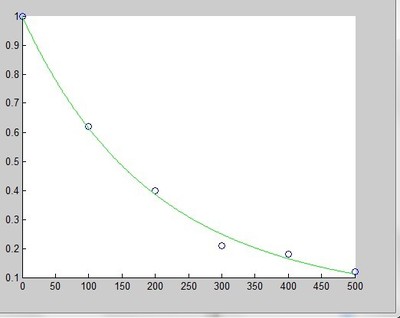
一元分段函数图

2.二元分段函数绘图

例如：

把下面的函数保存为Piecewise_xy.m文件

functionPxy=Piecewise_xy(x,y)
Pxy=0.5457*exp(-0.75*y^2 - 3.75*x^2 -1.5*x).*(x+y>1)+...
0.7575*exp(-y^2 - 6*x^2).*(x+y>-1)+...
0.5457*exp(-0.75*y^2 - 3.75*x^2 +1.5*x).*(x+y<=-1);
end

运行：

[x,y]=meshgrid(-3:0.1:3);
s=size(x)
Pxy=zeros(s(1),s(2));
for i=1:s(1)
forj=1:s(2)
Pxy(i,j)=Piecewise_xy(x(i,j),y(i,j));
end
end
mesh(x,y,Pxy)

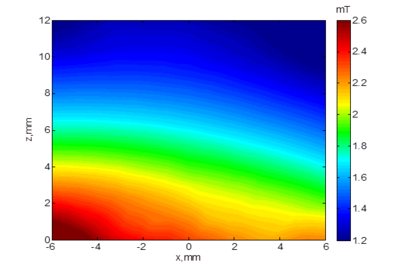
二元分段函数图

举例如下：

在matlab中，>>x1=0:0.01:1;
>>x2=1:0.01:2;

>> y1=x1;
>> y2=2-x2;
>> x=[x1,x2];
y=[y1,y2];
plot(x,y)

4例2

0<t<1 u(t)=0
其他时候u(t)=1
这个用matlab语言怎么定义函数u

如下：

function myfun(t) if 0<t && t<1 u=0 else u=1 end 输入myfun(8),可以得到结果

例3

比如说y=5/cos(x),我想绘制此曲线.但是x的定义域中不能包括1/2*pi和3/2*pi,怎样才能定义x,可以在除x=1/2*pi和3/2*pi以外绘制区间为[0,2*pi]的曲线. 谢谢各位厉害的大虾帮忙. 尽量写得详细一些.

如下：

>> x=0:.001:2*pi; >> c=.1; >> y=5./cos(x); >> y(abs(x-pi/2)<c | abs(x-3*pi/2)<c)=NaN; >> plot(x,y);

例4 比较经典的一个分段函数绘图例子

x=-3:0.01:3;
y1=zeros(size(x));
y2=zeros(size(x));
y3=zeros(size(x));
N=length(x);
for k=1:N
if x(k)<-1&x(k)>=-3;
y1(k)=(-x(k).^2-4*x(k)-3)/2;
elseif x(k)>=-1&x(k)<1 ;
y2(k)=-x(k).^2+1;
else x(k)<=3&x(k)>=1 ;
y3(k)=(-x(k).^2+4*x(k)-3)/2;
end
end
y=y1+y2+y3;
plot(x,y)

爱华网本文地址 » http://www.413yy.cn/a/25101015/252716.html