一、 实验题目
设有n位选手参加网球循环赛,循环赛共进行n-1天,每位选手要与其他n-1位选手比赛一场,且每位选手每天必须比赛一场,不能轮空。试按此要求为比赛安排日程。
二、实验目的
1.深刻理解并掌握“分治算法”的设计思想;
2.提高应用“分治算法”设计技能;
3.理解这样一个观点:用递归方法编写的问题解决程序具有结构清晰,可读性强等优点,且递归算法的设计比非递归算法的设计往往要容易一些,所以当问题本身是递归定义的,或者问题所涉及到的数据结构是递归定义的,或者是问题的解决方法是递归形式的时候,往往采用递归算法来解决。
三、实验要求
1.实现《网球循环赛》问题的分治算法,并进行算法时间复杂性分析。
2.对实现的分治算法进行改进;
3.对上述改进后算法进行时间复杂性分析,通过实验结果分析对比,得出自己的结论和总结。
四、实验过程
1、算法一:
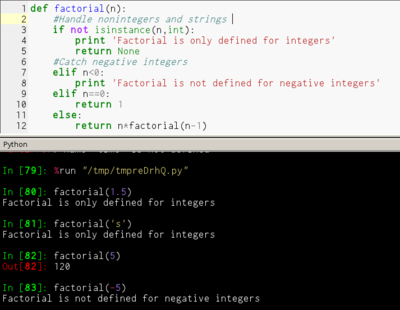
#include<stdio.h>
#define N 64
void GameTable(int k,int a[][N])
{
//n=2^k(k>=1)个选手参加比赛,二维数组a表示日程安排,数组下标从1开始
int n=2;//k=0,两个选手比赛日程可直接求得
//求解两个选手比赛日程,得到左上角元素
a[1][1]=1;a[1][2]=2;
a[2][1]=2;a[2][2]=1;
int i,j,t;
for(t=1;t<k;t++)//迭代处理,依次处理2^2,....,2^k个选手比赛日程
{
int temp=n;n=n*2;
//填左下角元素
for(i=temp+1;i<=n;i++)
for(j=1;j<=temp;j++)
a[i][j]=a[i-temp][j]+temp;//左下角 元素和左上角元素的对应关系
//将左下角元素抄到右上角
for(i=1;i<=temp;i++)
for(j=temp+1;j<=n;j++)
a[i][j]=a[i+temp][(j+temp)%n];
//将左上角元素抄到右下角
for(i=temp+1;i<=n;i++)
for(j=temp+1;j<=n;j++)
a[i][j]=a[i-temp][j-temp];
}
for(i=1;i<=n;i++)//显示日程表
for(j=1;j<=n;j++)
{
printf("- ",a[i][j]);
if(j==n)
printf("n");
}
}
void main()
{
int a[N][N];
int k;
printf("输入选手的个数:(注意为2的平方)");
scanf("%d",&k);
GameTable(k,a);
}
2、结果验证
当两个选手,即k=1时
当4个选手时,即k=2
当8个选手,即k=3
当16个选手时,即k=16
时间复杂度分析:
迭代处理的循环体内部3个循环语句,每个循环语句都是一个嵌套的for循环,且它们的执行次数相同,基本语句是最内层循环体的赋值语句,即填写比赛日程表的元素。基本执行语句的执行次数是:
T(n)=
所以时间复杂度为O(4k)
改进的算法:
#include<iostream>
using namespacestd;
const int SIZE =50;
inta[SIZE][SIZE];
void copy(intn);
void tournament(int n);
int odd(int n);//判断奇偶性
void makecopy(int n);//makecopy与copy算法类似,但是区分了n/2为奇数或偶数的情形
void copyodd(intn); //实现n/2为奇数时的复制
voidmain()
{
intn;
inti,j;
cin >>n;
tournament(n);
if(odd(n))// n为奇数和偶数输出情况不同,要分别考虑
{
for(i = 1; i<=n;i++)
{
for(j = 1; j<=n+1;j++)
if(a[i][j] ==n+1)
cout <<"0";
else
cout << a[i][j]<< "";
cout <<endl;
}
}
else
{
for(i = 1; i<=n;i++)
{
for(j = 1; j<=n;j++)
cout << a[i][j]<< "";
cout <<endl;
}
}
}
void copy(intn)
{
int m =n/2;
for(int i = 1; i<=m;i++)
for(int j = 1; j<=m;j++)
{
a[i][j+m] = a[i][j] +m;
a[i+m][j] =a[i][j+m];
a[i+m][j+m] =a[i][j];
}
}
void tournament(intn)
{
if(n ==1)
{
a[1][1] =1;
return;
}
if(odd(n))
{
tournament(n+1);
return;
}
tournament(n/2);
makecopy(n);
}
int odd(intn)
{
if(n%2==1)
return1;
else return 0;
}
void makecopy(intn) //makecopy与copy算法类似,但是要区分n/2为奇数或偶数的情形
{
if(n/2 > 1 &&odd(n/2))
copyodd(n);
else
copy(n);
}
void copyodd(intn)//实现n/2为奇数时的复制
{
intb[SIZE];
int m =n/2;
for(int i = 1; i<=m;i++)
{
b[i] =m+i;
b[m+i] =b[i];
}
for(i = 1; i<=m;i++)
{
for(int j=1; j<=m+1;j++)
{
if(a[i][j] >m)
{
a[i][j]=b[i];
a[m+i][j] = (b[i] +m)%n;
}
else
a[m+i][j] = a[i][j] +m;
}
for(j = 2; j<=m;j++)
{
a[i][m+j] =b[i+j-1];
a[b[i+j-1]][m+j] =i;
}
}
}
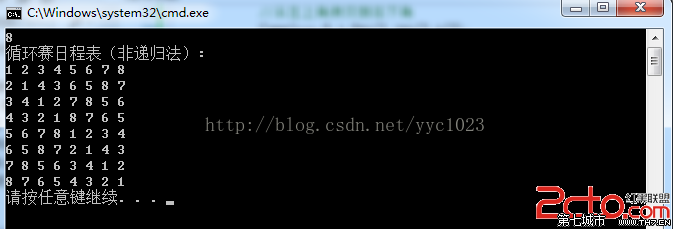
结果验证:
当参赛人数为偶数 8时
当参赛人数为奇数 7时
时间复杂度:O(4k)
 爱华网
爱华网