关于地球公转速度的估算报告
行星是以向心力与离心力在时间中(先后次序)相等的条件下,围绕太阳以椭圆轨道公转的。可以形象的比喻成警察用警绳拴住小偷的情景,小偷总想跑开,这是离心力,警察把他拉回,这是向心力。因此,可以这样说,从一个生活的侧面,警察抓小偷的故事为我们讲述了一个宇宙起源的传说。而牛顿苹果落地的故事讲的是科学起源的传说。
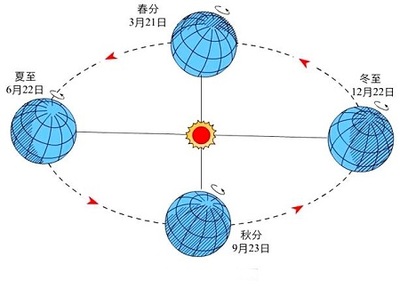
图1 地球公转轨道示意图
按牛顿的理论, 没有引入向心或离心平均速度的概念, 所以,一般计算行星在椭圆公转轨道不同点上的速度,都采用机械能角动量守恒原理估算,本文提出行星向心和离心平均速度的概念,并根据观测数据对行星公转速度作出估算。
地球公转轨道偏心率为0.0167,半长径a和半短径b分别为:
半长径a=0.999831*1.496*10^11(米)=1.495747176*10^11(米),
半短径b=a*√(1-e^2)=1.495747176*10^11*√(1-0.0167^2)=1.495538587*10^11(米)
平均圆半径:R=(a+b)/2=1.495642882*10^11(米)
平均圆半R与短半径b差 ΔL=(R-b) =10429500(米), 地球平均公转速度:V=29790(米/秒)
地球圆轨道的平均向心或离心加速度:±g=V^2/R=5.933529392*10^-3(米/秒^2)
按图1地球在A点1/4周期做加速运动达到B点, 在1/4周期作减速运动达到C点. 地球在
A→C点沿椭圆行程比平均圆行程少近似等于ΔL, 由C到D做减速运动,由D郅A做加速运动,沿椭圆行程C→A比平均圆行程多近似等于ΔL按公式:
ΔL=g*t^2/2=t*V/2
式中V/2是平均向心或离心速度,
需时间 t=√(2*ΔL/ g),t=√(20859000/5.933529392*10-3)=59291(秒)
地球公转周期T=365.256*24*60*60=31558118.4(秒), 取T/2±t, 分别为:
T1=T/2-t=15779059.2-59291=15719768 (秒),
T2=T/2+t=15779059.2+59291=15838350(秒)
按平均圆半径R计算半周长为L/2:
L/2=π*R=3.1416*1.495642882*10^11=4.698711678*10^11(米)
因此有地球在A→C点上最大平均速度为
V1=(L/2)/T1=29890.5 (米/秒)
地球在C→A点上最小平均速度为
V2=(L/2)/T2=29666.7(米/秒)
即求出地球平均公转速度V=(V1+V2)/2=29778.6(米/秒), 这与观测值误差仅为千分之三。
 爱华网
爱华网



