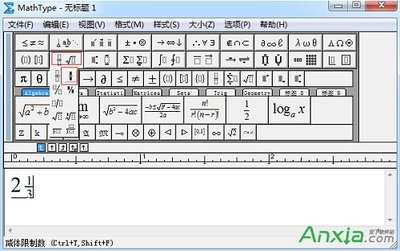
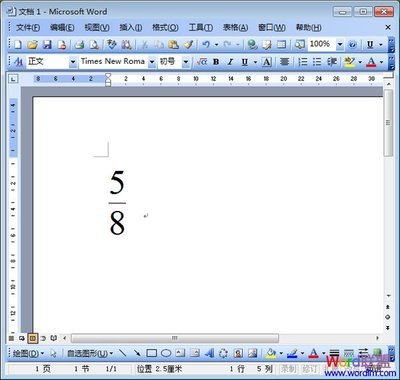
连分数(continuedfraction)是特殊繁分数。如果a0,a1,a2,…an,…都是整数,则将分别称为无限连分数
和有限连分数。可简记为a0 ,a1,a2,…,an,…和a0,a1,a2,…,an。一般一个有限连分数表示一个有理
数,一个无限连分数表示一个无理数。如果a0,a1,a2,…,an,…都是实数,可将上述形式连分数分别叫无限
连分数和有限连分数 。近代数学的计算需要,还可将连分数中的a0,a1 ,a2,…,an,…取成以x为变元的多
项式。在近代计算数学中它常与某些微 分方程式差分方程有关,与某些递推关系有关的函数构造的应用相联系。
有限连分数
所有有限连分数都表示一个有理数,而所有有理数都可以按两种不同的方式表示为有限连分数。这两种表示除了
最终项之外都是一致的。在较长的连分数表示,其最终项是 1;较短的表示去掉了最后的 1,而向新的终项加
1。在短表示中的最终项因此大于 1,如果短表示至少有两项的话。
无限连分数
所有无限连分数都是无理数,而所有无理数可用一种精确的方式表示为无限连分数。

无理数的无限连分数表示是非常有用的,因为它的初始段提供了对这个数的优异的有理数逼近。这些有理数
可以叫做这个连分数的收敛(convergent,也译为“渐进”)。所有偶数编号的收敛都小于最初的数,而奇数编
号的收敛都大于它。
 爱华网
爱华网