综合训练试题一 本中心备考武汉外校小升初，奥数杯赛，数学兴 武汉外校小升初试卷

本中心备考武汉外校小升初，奥数杯赛，数学兴趣辅导的综合训练试题（一）

电话15337245165QQ：258155493童老师奥数。

1、 将数字2、3、4、5、6、7、8、9这8个数，放在长方体的8个顶点上，使得6个面上每一个面上任意三数之和不小于13。那么一个面上四数之和的最小值是多少？

2、马戏团的猴子骑车节目是由5辆自行车来表演的，每只猴子至少骑一次车，但一只猴子不能重复骑同一辆车，表演结束后，5只猴子分别骑了2，2，3，5，X次，五辆车分别被骑了1,1,2,4,次。那么X+Y=（）。

3、一台天平，左盘上有若干个重量相等的黑球，右盘上有若干个重量相等的白球。这时两边平衡。现在从右盘上取走1个白球置于左盘上，再把左盘的两个黑球置于右盘上，同时给左盘加20克砝码，这时两边也平衡；如果从右盘移两个白球到左盘上，从左盘移1个黑球到右盘上，则需要再放50克砝码于右盘上，两边才平很，你知道白球，黑球每个各重多少克吗？

4、有两堆棋子，甲堆有350颗黑子和500颗白子。乙堆有400颗黑子和100颗白子。为了使甲堆中黑子占50%，乙堆中黑子占75%。要从乙堆中拿多少黑子给甲堆？从乙堆拿多少白子给甲堆？（仅限算式方法）

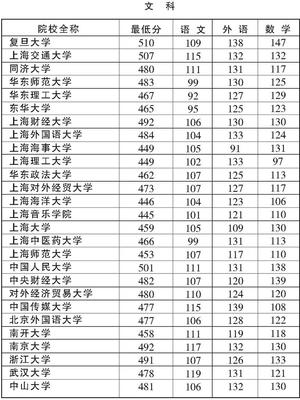
5、一次考试一共有10道判断题，正确的打勾，错的打叉，每道题目10分，满分为100分。甲乙丙丁4名同学的解答及甲乙丙三名同学的得分如下表表示。丁应得多少分？

6、5个空瓶可以换得一瓶汽水，某班同学喝了161瓶汽水，其中有一些是用喝剩下来的空瓶换的，那么他们至少要买汽水多少瓶？

7、在一个圆周上有8个点，正好把圆周分成八等分，以这些点为顶点作三角形，可以作出多少个等腰三角形。

8、老师在黑板上写下3个数：108,396，A。让同学们求它们的最小公倍数。马小哈将108错当成180进行计算。结果竟然与答案完全一致。A的最小值为多少？

9、某人从住地外出有两种方案，一种是骑自行车去，另一种是乘公共汽车去。显然乘公共汽车的速度比骑自行车的速度快，但乘公共汽车有一个等候时间。（后撤时间可以看作是固定不变的）。在任何请款下，他总是采用花时间最少的方案。下表表示他到达A、B、C三地采用最佳方案所需要的时间。

10、甲乙丙3个人玩3张牌。这3张牌分别写着不同的自然数。洗牌后发给每个人1张。按照每个人所拿的自然数得分，一共玩了3次以后，甲19分。乙和丙各得13分。那么这3张牌上写的数依次是（）、（）、（）。

11、从张村到王庄的路有上坡、下坡及平路，全程14千米/小时。如果上坡的速度是3千米每小时。下坡是6千米每小时。平路是5千米每小时。那么从张村到王庄需要3.5小时。而从王庄原路返回张村需要3小时。问：从张村到王庄的路程中，上坡、下坡、平路各是多少千米？

12、甲乙两个人同时从山脚开始爬山，到达山顶后就立即下山，他们两个人下山的速度都是各自上山速度的2倍。甲到达山顶时乙距离山顶还有400米。甲回到山脚时乙刚好下到半山腰，求山脚到山顶的距离？

13、某校办工厂生产3种棋，每种棋盘都是长方体，尺寸见下表（单位：厘米。）如果涉及一种长方体包装箱，使得不论哪一种棋都能正好装满。这种长方体包装箱的容积至少是多少立方厘米？

①象棋的长宽高分别是24、15、3；

①陆战棋长宽高分别是20、12、2；

③飞行棋长宽高分别18、10、2；

14、有若干个自然数，平均值是10，若从这些数中去掉最大的一个，则余下的平均值为9；若去掉最小的一个，则余下的平均值为11。问：（1）这些数最多有几个？（2）这些数中最大的数最大能是几？

15、利民商店从日杂公司买进一批蚊香，然后按希望获得的纯利润每袋加价40%定价出售。但是，按照这种定价卖出这批蚊香的90%时。夏季即将过去。为加快资金周转，商店以定价打七折的优惠价，把剩余的蚊香全部卖出。这样实际上获得的纯利润比希望获得的纯利润少了15%。按照规定，不论按照什么价格出售，卖完这批蚊香必须上缴营业税300元。（税金和买蚊香用的钱一起作为成本）。问利民商店买进这批蚊香用了多少元？

16、数学竞赛团体奖的奖品是10000本数学课外读物。奖品发给前五名代表队所在的学校。名次在前的代表队获奖的本数多，且每一名次奖品的本数都是100的整数倍。如果第一名所得的本数是第二名与第三名所得的本数之和。第二名所得到的本数是第四名和第五名所得到本数之和。那么，第三名最多可以得到多少本？

17、小明用了5天时间看完了一本200页的故事书。已知第二天看的页数比第一天看的页数多。第三天看的页数是第一、二天两天看的页数之和。第四天看的页数是第二、三天看的页数之和。第五天看的页数是第三、四天看的页数之和。那么小明第五天至少看了多少页？

18、一项工作，甲队单独完成比两项合作完成要多用16天。乙队单独完成要比两队合作完成多用9天。求如果按照甲队做一天。乙队做一天的顺序去完成，一共需要多少天？

19、一项工程，甲队单独完成的时间是乙、丙合作完成时间的2倍。乙队单独完成的时间是甲、丙合作完成时间的5倍。已知甲队单独完成这项工程比丙队单独完成要多用10天。那么乙队单独完成这项工程要多少天？

20、甲、乙两个代表团乘车去参观，每辆车可以乘36人。两代表团坐满若干辆车后，甲代表团余下的11人与乙代表团余下的成员正好又坐满一辆车。参观后，甲代表团的每个成员与乙代表团的每个成员两两合拍一张照片留念。那么拍完最后一张照片后。照相机里的胶卷还可以拍多少张照片？（每个胶卷可以拍36张照片。）

21、某住宅区有12家住户。他们的门牌号分别为1,2,3,4.......，12，他们的电话号码依次是12个连续的6位数。并且每家的电话号码都能被这家的门牌号整除。已知这些电话号码的首位数字都小于6。并且门牌为9的这一家电话号码也能被13整除。请问这一家的电话号码是多少？

22、一个长方体木块长为30厘米，宽为20厘米。高为25厘米。先在这块木块上截下一个尽量大的正方体，再用剩下的材料截出一个体积尽量大的圆柱体。这个圆柱体的体积是多少立方厘米？

23、有一路电车从甲站开往乙站，每五分钟发车一趟。全程需要15分钟，小张从乙站骑自行车沿着电车线去甲站。出发时恰好有一辆电车到达乙站。在路上又遇到8辆迎面开来的电车，到达时恰好有一辆电车从甲站出发，他从乙站到甲站一共多少分钟？

24、游客在9时15分由码头划出一条小船。他欲在不迟于12时回到码头，河水的流速为每小时1.4千米。小船在静水中的速度为每小时3千米。他每划30分钟就要休息15分钟，中途不改变方向，并在某此休息后立即往回返。他最多能划离码头（）千米。（假设休息时船在原地抛锚不动）

25、甲乙两船分别在一条河的AB两地同时相向而行，甲顺流而下，乙逆流而行。相遇时，甲乙两船行了相等的航程，相遇后继续前进，甲到达B地，乙到达A地后，都立即按原来路线返航，两船第二次相遇时，甲船比乙船少行1千米。如果从第一次相遇到第二次相遇时间相隔1小时20分。则河水的流速为每小时多少千米？

26、姐弟俩正要从公园门口沿着马路往东边去某地。他们回家要从公园门口沿着马路向西行，他们商量是先回家取车再骑车向东去某地省时间，还是直接从公园门口步行向东去省时间。姐姐算了一下：已知骑车与步行的速度比是4:1，从公园门口到达某地距离超过2千米时，回家取车才合算。那么，公园门口到他家的距离有多少米？

爱华网本文地址 » http://www.413yy.cn/a/25101015/248227.html