一、教材的地位、作用及前后联系
本节课的内容属于空间与图形领域,是在学生认识并掌握了长方体和正方体的基本特征的基础上进行教学的。计算长方体和正方体的表面积在生活中有广泛的应用,学习这部分内容,可以加深学生对长方体和正方体特征的理解,解决一些有关的实际问题。同时,还可以使学生对自己周围的空间和空间中的物体形成初步的空间观念,是进一步学习其他立体几何图形的基础。
二 教材的编写意图
表面积这部分内容,是在学生认识并掌握了长方体和正方体特征的基础上教学的。教学的难点在于,学生往往因不能根据给出的长方体的长、宽、高,想像出每个面的长和宽各是多少,以致在计算中出现错误。为了使学生更好地建立表面积的概念,教材加强了动手操作,让每个学生拿一个长方体或正方体纸盒,沿着棱剪开,再展开,看一看展开后的形状。然后,让学生在展开后的图形中,分别用“上”“下”“前”“后”“左”“右”标明6个面。这样,可以使学生把展开后每个面与展开前这个面的位置联系起来,更清楚地看出长方体相对的面的面积相等,每个面的长和宽与长方体的长、宽、高之间的关系,为下面学习计算长方体的表面积做好准备。在这以后,概括出表面积的含义。
例1和例2,分别教学长方体和正方体表面积的计算方法。例1先引导学生明确,要知道至少用多少平方米的硬纸板,实际上就是求这个长方体包装箱的表面积,然后根据所给出的微波炉包装箱的长、宽、高,确定每个面的长和宽各是多少,想出每个面的面积应该怎样算。然后,再列出计算表面积的式子,让学生计算。为了培养学生能够根据具体条件和要求,确定不同的面的面积怎样算,更好地发展空间观念,教材中没有总结长方体表面积的计算公式,而是让学生根据表面积的概念自己计算。在例1的基础上,例2启发学生自己根据正方体的特征,想出正方体表面积的计算方法。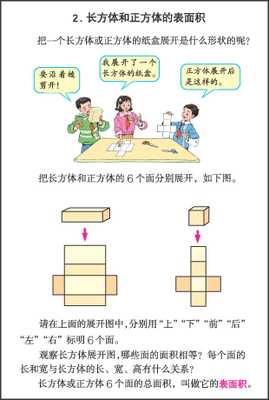
实际生活中,经常遇到不需要算出长方体6个面的总面积的情况。例如,制作没有盖的鱼缸、木箱或铁桶,粉刷房间的墙壁等,就需要根据具体情况考虑应该计算哪几个面的面积。教材通过教科书第34、35页的“做一做”加以说明,并且在练习中也适当加强了这方面的练习
由于根据长方体的长、宽、高来确定各个长方形面的长和宽,对小学生来说是个难点。教材在练习六中采取分步走的办法,逐步使学生掌握。第1题,先练习求一个指定面的面积,这样可以帮助学生根据直观图所给的条件,逐步弄清计算的是哪个面的面积,这个面的长和宽应该是多少,哪些面的面积相等,进而逐步掌握计算长方体、正方体表面积的方法。
三、学情分析。
小学五年级的学生的思维能力主要是直观形象到逻辑思维的过渡阶段。他们有一定的空间观念和动手能力,对长方体和正方体也已经有了一些初步的认识,掌握了它们的基本特征。要想理解长方体和正方体表面积的计算方法,必须理解每个面的长和宽各是多少。学生往往因不能根据给出的长方体的长、宽、高想象出每个面的长和宽各是多少,以致在计算中出现错误。为此,教学中加强了让学生动手操作和通过对长方体和正方体实物的观察,来突破难点。
四 教学目标及重、难点。
基于以上的分析,我认为这一教学内容的教学目标是
1、结合具体情境使学生知道什么是长方体、正方体的表面积,在理解概念的基础上初步掌握长方体、正方体表面积的计算方法;2、发展学生的空间观念,培养学生的分析、概括能力。3、培养学生自主探索的意识。教学重点:掌握长方体、正方体表面积的计算方法,能解决简单的实际问题。教学难点:根据给出的长方体的长、宽、高,确定每个面的长和宽,这也是本节课的关键。
五、教学实施的思考。
基于以上的教材解析及学情分析,我认为在教学实施的过程中我们应该这样做:
一关注学生观察、思维、实践能力的培养。
在教学长方体和正方体表面积时,让学生在课前收集大小不同的长方体物件,以制作这些物体需要多少材料这个实际问题入手展开教学,然后让学生思考,想办法,动手剪,展开后求出展开图的总面积即可,从而揭示表面积的概念。学生对学习材料本身是非常熟悉的,因而感到很有兴趣,在课堂教学中保持着比较活跃的思维状态。课 堂教学目标的实施非常顺利。课后,布置学生进行课外实践作业,寻找生活中的长方体物件,分析制作这个物件需要材料的多少与长方体、正方体表面积计算的联系。有利于培养学生观察、思维、实践能力。
二 抓住事物的本质特征展开教学
在教学表面积的计算方法时注意引导学生依据长方体和正方体的面的特征展开教学。通过对长方体正方体教具的观察、测量、计算来体验探究表面积的整个过程。在教学过程中,还结合学具,让学生在长方体、正方体学具上标出长、宽、高,然后思考相对的面面积怎么求,从而让学生养成一一对应的数学思想。
三 联系生活实际解决问题
为了培养学生解决问题的灵活性,应该设计多个与生活息息相关的素材,如要制作一个电视机罩需要多少布、制作一个金鱼缸需要多少玻璃、一个牛奶盒要包装四周需要多大的包装纸等等,让学生根据实际情况思考到底要求哪几个面的面积总和,然后选择有关数据进行计算,灵活解决实际问题,而不是死板的运用知识。
 爱华网
爱华网
