初三数学：圆-四点共圆的证明

七个基本判断方法集结

1. 若四个点到一个定点的距离相等，则这四个点共圆
2. 若一个四边形的一组对角互补（和为180°），则这个四边形的四个点共圆
3. 若一个四边形的外角等于它的内对角，则这个四边形的四个点共圆
4. 若一个点在一条线段的同旁，并且和这条线段的两端连线所夹的角相等，那么这两个点和这条线的两个端点共圆
5. 若AB、CD两线段相交于P点，且PA×PB=PC×PD，则A、B、C、D四点共圆(相交弦定理的逆定理)
6. 若AB、CD两线段延长后相交于P。且PA×PB=PC×PD，则A、B、C、D四点共圆(割线定理)
7. 若四边形两组对边乘积的和等于对角线的乘积，则四边形的四个顶点共圆(托勒密定理的逆定理)

图解

1.若四个点到一个定点的距离相等，则这四个点共圆

若可以判断出OA=OB=OC=OD，则A、B、C、D四点在以O为圆心OA为半径的圆上

【对于例题】：2010年海淀区初三一模数学25题

本题中涉及到PB=PC=PD=PM则B、C、D、M四点共圆

2.若一个四边形的一组对角互补（和为180°），则这个四边形的四个点共圆

如图

若∠A+∠C=180°或∠B+∠D=180°，则点A、B、C、D四点共圆

【对应例题】2010-2011学年海淀区初三上学期期末数学测试第25题

3.若一个四边形的外角等于它的内对角，则这个四边形的四个点共圆

若∠B=∠CDE，则A、B、C、D四点共圆

4.若一个点在一条线段的同旁，并且和这条线段的两端连线所夹的角相等，那么这两个点和这条线的两个端点共圆

若∠A=∠D或∠ABD=∠ACD，则A、B、C、D四点共圆
【证明点击博文】http://blog.sina.com.cn/s/blog_673b31580101hbic.html
【对于例题】例题中第（2）问证明可以用四点共圆方法证明（也可以选择中信+倍长的方法）

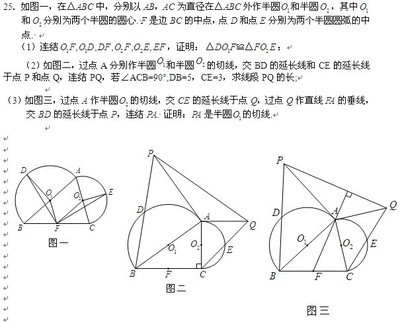
6.若AB、CD两线段延长后相交于P。且PA×PB=PC×PD，则A、B、C、D四点共圆

爱华网本文地址 » http://www.413yy.cn/a/25101015/245737.html