基尔霍夫电压定律(Kirchhoff's voltagelaw,KVL)用来确定回路中各段电压的关系.基尔霍夫电压定律指出:任一瞬时,如果从回路中任意一点出发,以顺时针方向或逆时针方向沿回路循环一周,则在这个方向上的电压降之和等于电压升之和,即任一瞬时,沿任一回路循环方向,回路中各段电压的代数和恒等于零:
∑U = 0
一个电路如果选定了参考点,那么回到原来的出发点时,该点的电位不会发生变化,这是电路中任意一点的瞬时电位具有[单值性]的结果.
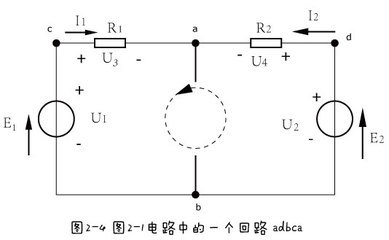
以图2-4所示的回路(即为图2-1所示电路的一个回路)为例,图中电源电动势、电流和各段电压的参考方向均已标出。按照虚线所示方向循环一同,根据电压的参考方向可列出
U1+U4=U2+U3
或改写为
U1-U2-U3+U4=0
即
∑U=0(2-3)
就是说:在任一瞬时,沿任一回路循环方向(顺时针方向或逆时针方向),回路中各段电压的代数和恒等于零。电压的升降如果与绕行方向一致,则电压取正号;如果与绕行方向相反,则电压取负号。电压的升降一般与所设的电流的参考方向取关联参考方向。
图2-4所示的回路是由电源电动势和电阻构成的,上式可改写为
E1-E2-R1I1+R2I2=0
或
E1-E2=R1I1-R2I2
即
∑E=∑(RI)
这是基尔霍夫电压定律在电阻电路中的另一种表达式,即在任一回路循环方向上,回路中电动势的代数和等于电阻上电压降的代数和。其中,凡是电动势的参考方向与所选回路循环方向相反者,取正号,一致者则取负号。
KVL不仅适用于闭合电路,也适用于是开口电路;图2-5所示电路不是闭合电路,但在a,b开口端存在电压Uab,可假设一个闭合电路,若顺时针方向绕行,则KVL方程为
Uab-U2-U1=0
即
Uab=U1+U2
说明a,b两端开口电路的电压等于a,b两端另一支路各段电压之和,这反映了两点间电压与所选择路径无关
应该指出,图2-4所举的是直流电阻电路,但是基尔霍夫两个定律具有普遍性,它们适用于由各种不同元件所构成的电路。列方 程时,不论是应用于基尔霍夫定律还是欧姆定律,首先都要在电路图上标出电流、电压或电动势的参考方向;所列方程中各项前的正负号是由它们的参考方向决定的。若电路有含有受控源,仍要上述方法列方程式,但要在方程式中反映受控源的受控特性。
Example 2.2 Calculate thevoltage between terminal a and b(Fig.2-6).
Solution
First,useOhm's law to determine the value of I:
I=U1-E1/R1+R2=10-4/4+2=1A
Next,apply KVL at the open status circuit:
Uab=-E2+Ucd+Udb
Ucd=IR1+E1=1×4+4=8V
Udb=0
Finally,substitutethe value found for Ucd and Udb,yields(得出)
Uab=-2+8+0=6V
 爱华网
爱华网