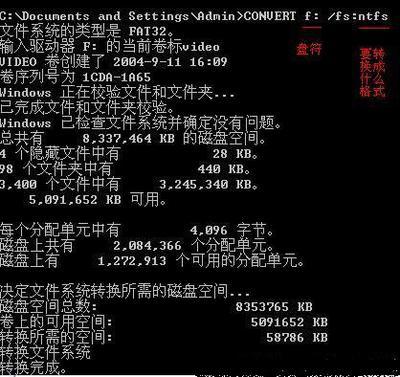
图1是一个AWGN信道,该信道的复噪声功率是1,信道复增益是2exp(j*pi/3)、幅度增益是2、功率增益是4。假设发送功率是1,则该信道的容量是ln5(nats/channeluse)。达到容量的必要条件包括:x~CN(0,1)。
图1
图2是两个独立的AWGN信道,假设总发送功率还是1。如果发端匀分功率,则每路的发送功率是0.5,总容量是ln4.5nats/channel use。如果发端对功率进行优化分配,则总容量可以推 算出是ln5.0625
图2
图2中的信道增益的相位不影响容量,故当我们谈论容量问题时,可以去掉。另外,我们还可以用向量矩阵的方式,使图2成为更紧凑的图3。
图3
图3中的向量x、y、z都是列向量, S是对角阵diag([2,1])。如果图2中不是2条信道,而是N个信道,则S有N个非0的对角元素。图3用公式语言来表述就是
对图3中的向量分别做酉变换不改变容量,因此对于容量而言,图3和图4是等价的。图4中的U、V都是酉阵。图4中A点到B点的容量等于C点到D点的容量。
图4
噪声向量z是圆对称的,酉变换不改变其性质,因此图4和图5在容量问题上是完全等价的。
图5
图5中的三个矩阵相乘的结果可以记为一个矩阵:
因此,图5可以等效为图6。
图6
就是说,图6所示的矩阵信道和图2所示的两个(或多个)独立的AWGN信道是等效的。
然后我们来看MIMO信道的容量。任何一个窄带MIMO信道都可以用图6来表示。任何矩阵都存在SVD分解,所以任何MIMO信道都可以等效成图5。酉变换不改变容量,所以任何MIMO信道可以等效成图3。因此:MIMO信道的容量就是一组不同增益的AWGN信道的容量。
给定H时,求解MIMO信道容量的关键就是求解图5中对角阵S的对角线元素。数学中有标准的方法从H算出S。
假S设有R个非0元素,其中的第k个是h_k,假设总发送功率是P,每天线的噪声功率是s2,则该MIMO信道的容量
为(如果发端不做功率分配)
其中后一步来自数学中的等式。式中的P/Mt体现各个子信道均分功率。如果发端已知H,则应当考虑优化功率分配。
总而言之,一个多天线系统,表面上我们看见的是矩阵H。揭开它的面纱,我们发现里面隐藏着R个独立的信道。S就是被隐藏的独立信道,U和V操作相当于是收端和发端分别对S做出的隐藏行为。
 爱华网
爱华网