储油罐的变位识别与罐容表标定

杨茂松，周正龙，刘青

（北方民族大学信息与计算科学学院应用数学系，宁夏·银川750021）

摘要

随着社会经济的发展，机动车数量不断增加，加油站就显得尤为重要。为了满足人们的需求，并且做到“适用、安全、经济、美观”，加油站点越来越普及，其危险性也受到了越来越多的关注。加油站内危险性最大的部分为储油罐区，大部分加油站的储油罐为地下设置，但这也给进油和出油带来了不便，所以需要建立一个准确的配套“油位计量管理系统”。

对于问题一，利用数学中微积分的思想，建立了罐内油位计高度与储油量的方程模型。首先，在罐体无变位的情况下建立了初级模型。其次，对初级模型进行改进并建立了函数的最佳平方逼近模型，然后给出了储油量与油位高度对应数据表格，用直接查表法即得数据，进而给加油站人员提供很大便利。最后，对模型进行了检验和误差估计，然后采用MATLAB软件，对附件1中所提供的数据进行筛选，并从中随机抽取4组数据（每组5个采样），对实验数据进行最小二乘法拟合，得到储油量随油位高度变化的情况。之后进一步论述了罐体变位后罐内油位高度与储油量的关系，在初级模型的基础上建立了等价代换变位模型，用微积分知识求得体积对高度的函数，再通过MATLAB程序运行，而得到罐体变位前后油位高度间隔为1cm的罐容表标定值。进而通过对两种情况的对比，得出罐体变位后对罐容表的影响，同时说明了在等梯度油位高度下，变位后的储油体积变化较快。

对于问题二，在问题一的基础上，充分考虑到油罐形状，将其分为两部分（圆柱体和两球冠组成的椭球体），并用方程模型求得两部分的体积之和，然后根据体积不变原理，建立变位后罐内储油量与油位高度及变位参数之间的模型。再利用MATLAB软件及Excel对相关数据处理后，从而得出和的值，并根据所建立的数学模型，给出罐体变位后油位高度间隔为10cm的罐容表标定值。最后将附件2中的实际检测数据与所求的相应数据进行比较，结果与实际基本吻合，从而验证了所建模型的正确性与可靠性。

关键词：微积分；最佳平方逼近法；MATLAB软件；罐容表标定；等价代换变位模型

一、问题重述

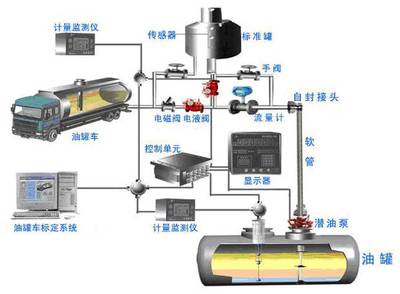
随着社会经济的发展，机动车数量不断增加，加油站就显得尤为重要。加油站内危险性最大的部分为储油罐区，大部分加油站的储油罐为地下设置，但这也给进油和出油带来了不便，所以建立一个配套的“油位计量管理系统”尤为重要，本题采用流量计和油位计来测量进油量、出油量与罐内油位高度等数据，通过预先标定的罐容表（即罐内油位高度与储油量的对应关系）进行实时计算，以得到罐内油位高度和储油量的变化情况。

由于地基变形等原因，许多储油罐在使用一段时间后，使罐体的位置会发生纵向倾斜和横向偏转等变化（即变位），从而导致罐容表发生改变。按照有关规定，需要定期对罐容表进行重新标定。图中给出了一种典型的储油罐（主体为圆柱体，两端为球冠体）和一种小椭圆型储油罐（两端平头的椭圆柱体）的尺寸及形状示意图。图2是其罐体纵向倾斜变位的示意图，图3是罐体横向偏转变位的截面示意图。

请用数学建模方法研究解决储油罐的变位识别与罐容表标定的问题。

（1）为了掌握罐体变位后对罐容表的影响，利用如图4的小椭圆型储油罐，分别对罐体无变位和倾斜角为的纵向变位两种情况做了实验，实验数据如附件1所示。请建立数学模型研究罐体变位后对罐容表的影响，并给出罐体变位后油位高度间隔为1cm的罐容表标定值。

（2）对于图1所示的实际储油罐，试建立罐体变位后标定罐容表的数学模型，即罐内储油量与油位高度及变位参数（纵向倾斜角度和横向偏转角度 ）之间的一般关系。请利用罐体变位后在进/出油过程中的实际检测数据（附件2），根据所建立的数学模型确定变位参数，并给出罐体变位后油位高度间隔为10cm的罐容表标定值。进一步利用附件2中的实际检测数据来分析检验你们模型的正确性与方法的可靠性。

二、问题分析

通常加油站都有若干个储存燃油的地下储油罐，并且一般都有与之配套的“油位计量管理系统”，采用流量计和油位计来测量进/出油量与罐内油位高度等数据，通过预先标定的罐容表（即罐内油位高度与储油量的对应关系）进行实时计算，以得到罐内油位高度和储油量的变化情况。本文主要研究解决储油罐的变位识别与罐容表标定的问题。附件1是罐体无变位和倾斜角为的纵向变位的实验数据，数据的特点是不同时段不同油位高度累计进出油量的值，而要解决的是实际储油量随油位高度变化的情况，所以要对数据进行处理。附件2是一定时间内采集某加油站实际储油罐的检测数据，是用来检验所建立模型的正确性和方法的可行性。

2.1问题一的分析

对于问题一，主要是对罐体两种状态（无变位和变化一定角度）下，储油量随油位高度变化的比较，进而得出罐体变位对罐容表的具体影响。此问题的关键就是求油位高度为时，两种状态下的储油体积与油位计读数关系，可以从数学分析中微分的思想，解决此类问题，数学中常用方法有穿针引线法和切片法求重积分进而求出相应的体积。

首先，用定积分求体积公式建立罐体无变位的方程模型，由变位后储油体积不变原理，油位计在油罐变位后的读数总与一个标准型的高度相对应，然后利用等价代换的思想，求得罐体变位后的体积关于高度的方程模型。最后求得变位前后油位高度间隔为1cm的罐容表标定值，得出对罐容表的具体影响的结论。再将附件1的实验数据值与所求得的结果进行对比，验证模型的合理性和适用性。

2.2问题二的分析

对于问题二，结合实际储油罐的形状特点给出罐体变位后罐容表标定值。问题二第一问是要建立罐内储油量与油位高度及变位参数， 之间的关系式，此问题与问题一中模型类似，在此不再赘述。而第二个问题是利用附件2中实际数据进行分析并通过中心差分方法和均值法将数据中罐体变位后油位高度与罐容体积分两大类，且求得每组的计算值，之后通过该计算值可带入相应模型求得变位参数。再进一步利用MATLAB等相关数学软件可求得相应的油表标定值，从而以标定值为准，用标定值的变化可以说明实际生活中加油站的油量预测，进而反映加油站的一些相关问题。

三、模型假设

1.假设在一段时间内，忽略温度和压强的影响，地下储油罐自身不会变形。

2.假设加油站选址现场的实际地形、地况、地质勘测良好。

3.不考虑地震等自然现象对储油罐变位带来的影响。

4.在一段时间内不考虑燃油的挥发情况。

5.假设题目所给的数据真实可靠。

6.假设不考虑储油罐壁的厚度，可认为储油罐的体积和容积近似相等。

（注：上述假设是模型讨论过程中的部分假设，在后面的分步讨论中可能引入新的假设）

四、定义与符号说明

：椭圆储油罐的长半轴的长度；

：椭圆储油罐的短半轴的长度；

：椭圆储油罐的横向长度；

：椭圆储油罐的横截面的面积；

：某一时刻椭圆储油罐的储油体积

：某一时刻无变位时椭圆储油罐中的油位高度；

：某一时刻变位角度时椭圆储油罐中的油位高度；

：纵向倾斜角度；

：典型的储油罐的油位高度；

：某一时刻变位角度时实际储油罐中的油位高度；

：某一时刻变位角度时实际储油罐中的油位高度；

：某一时刻综合变位后实际储油罐中的油位高度；

（注：上述假设是模型讨论过程中的部分符号，在后面的讨论中可能引入新的假设符号）

五、模型的建立与求解

5.1模型的准备

5.11函数的最佳平方逼近^[1]

1.公式的推导

给定[a,b]上的连续函数f(x), 及子空间

所谓 在中的最佳平方逼近，就是存在

使得对于一切

都有：

此不等式说明，所求的

满足等式：

而

是由系数唯一确定的，因此，只要我们求出了满足上式的 就可以求出 最佳平方逼近：

2.误差的估计

最佳平方逼近的误差为

由

可得

于是在区间[a,b]上的最佳

5.2问题一的模型建立与求解

5.21初级无变位方程模型

分别以椭圆横截面的长轴、短轴所在直线为 轴和轴建立如图所示的直角坐标系，得到椭圆的方程为

图1

用 表示 的函数式为

为了求小椭圆型储油罐的体积，采用定积分求解^[2]。设椭圆阴影部分的面积为

则面积关于油位高度的表达式为

又由定积分求体积的计算公式得

具体数据处理时，主要应用MATLAB软件计算定积分，并给出在某油位高度下的油体积。，首先进行单位化统一都化为分米计算，其次采用分段抽样的方法筛选出一部分油位高度的数据，并赋值给h,在MATLAB程序^[3]（参见附录1）中运行求得对应的油体积列表如下。

表1

上表表明通过初级模型计算出的储油体积与附件1中的实验数据还存在一定的误差，并且算式里含有反正弦函数,在实际应用中计算起来不方便。由于用多项式计算简单方便, 下面我们用多项式逼近的方法给出改进的模型。

5.22改进模型

首先令，则有

因为函数在定义域 连续且存在一阶导数， 有界，所以 的契比晓夫级数为：

一致收敛于函数

其中

即得:

（*）

用函数的契比晓夫级数的部分和，即最佳平方逼近多项式:

代替

从（*）可得出在 上效果较好的V(x)的近似计算公式:

下面讨论的求法：

当为偶数时,由于 为偶函数,又 为奇函数， 为偶函数，可知中的被积函数为奇函数,又积分区间[-1,1]为对称的,因此

当为奇数时,设 ,则用分步积分法球的积分如下:

带入得到近似计算公式:

其中

当 时，用 代替

得到 的近似值为

当 时，用

代替 ,

得到 的近似值为

5.23改进模型的误差估计

近似计算误差估计式为

(注：推导过程请参考文献[1])

5.24改进模型的检验

在缺少计算工具的情况下，为解决实际问题，我们就可以通过直接查表的方式求得储油量，具体见下表。

表2

对近似数据与实验测得的数据进行比较，得知用这种方法还是存在误差的，但这是否影响最后的结果，改进模型是否适用和合理，通过以下的误差估计来说明。

需要结合题目数据给出具体的误差估计，结合题目中图4小椭圆形油罐的尺寸，即当时，计算出 的具体范围。为了简单起见，不妨取k=1,于是用 代替函数

经过上述检验，对于体积相对较大的储油罐来说，相对误差较小，从而验证了本模型的可行性，也为模型的合理性提供了有力依据。

5.25等价代换变位方程模型

在某一时刻，未进油和出油的时候，变位前后油罐中油的体积是不变的，即。又由图2的分析知，变为前后的油位高度存在一定的几何关系，即 。所以将 用的表达式等价替换得到变位后油量与罐内油位高度的关系式 如下

图2

数据处理处理过程同初级方程模型的过程，将单位统一化为米，主要应用MATLAB软件计算，在MATLAB程序^[4]中运行求得罐体变位后油位高度间隔为1cm的罐容表标定值如下表，并将无变位和变位时的数据作比较，分析罐体变位后对罐容表的影响。

由上表可以清晰地看到，当 的取值不同时，对应的罐容体积 也随着取不同的值，从而可以通过罐容体积 的变化来反映罐容表标定值的变化情况。而且根据变位后油位高度间隔为1cm时分别给出无变位出油标定值、变位后出油标定值。对比变位前后的标定值，得到变位后标定值的变化率要比变化前的标定值变化率大，即可以说明由于地基变形等原因引起罐体变位会引起罐容表标定值的改变。由于标定值的不准确，可能引发诸多问题。具体如下：

1.可能导致滴油现象发生而引发危险。

2.由于标定值不准确，可能导致给顾客的加油数量不准确，引起顾客不满，从而使营业额下降。

5.3问题二的模型建立与求解

5.31基础模型

在无变位的情况下建立模型，基于问题一的初级方程模型和图3的储油罐示意图，主体为圆柱体，两端为球冠体，油罐的体积是圆柱体体积与两球冠体积 之和，即 ，又两球冠组合在一起就是一个椭球体，所以建立如下图所示的直角坐标系。

它们的方程分别为

根据积分的知识，分别球的两部分体积如下。

其中

将x ,z代入得到

由此得到油罐的总体积

5.32变位模型

由问题一的等价代换变位方程模型，根据体积不变原理，变为前后的油位高度存在一定的几何关系，即 和分别给出纵向变为和横向变位后油罐体积的表达式^[5]

（纵向变位 角度的函数）

（横向变位 角度的函数）

当纵向变位和横向变位同时发生时，变位前后油位高度变化关系为

，即 ，从而得到变为后的体积

进而得出油的容积与油位计读数 、横向变位角 、纵向变位 的数学模型。

5.33确定变位参数

由于本模型是建立在理论知识基础上的，故需要利用相关数据来进一步模拟，从而得出和 的值，并根据所建立的数学模型，给出罐体变位后油位高度间隔为10cm的罐容表标定值。

首先，通过对附件2中所给数据的处理，可以从大量的数据中看出罐内油位高度 与显示油量成现一定的关系，故在通过对单位统一为米后，利用中心差分法对开始采集，到一次性补充进油的实际数据，到结束采集的实际数据进行处理，再进一步对这两组数据利用均值方法各取得两组数据，作为和 的具体结果，即有：

1）

2）、

3）

通过MATLAB和Excel等相关软件的计算和拟合，可以初步得到 和 的近似结果 如下：

从而通过解二元一次方程组（用MATLAB软件），求得相关的变位参数 和 分别为：

， 。

用MATLAB软件计算出油位高度间隔为10cm的罐容表标定值下表。

六、模型评价与不足之处

6.1模型评价

通过整个过程的模型建立，出于对模型的适用性、可靠性、推广性等，可以给出模型的相关优点，并加以利用，使之解决加油站的相关事件，更重要的是，可以进一步用于对加油站进出油的估计与准确测量，以便及时发现由于地形变位或人为因素带来的负面影响。当然，由于本模型本身由于忽略了某些客观因素（如：油罐的材料、温度的影响、罐的内外壁等），故模型的不足之处给出了相关小结。具体如下：

优点：

1、本模型的过程简洁，有力，深刻；

2、模型建立的思想比较简单，一气呵成，是数学中常见的积分方程；

3、改进模型可用直接查表法得出数据，有很强的实用性；

4、在数据处理过程中大部分采用MATLAB数学软件，大大简化了制图和计算工作；

5、通过附件1的数据对本模型进行检验，使模型变得可靠和有意义；

6、用等价代换方法将变位前后的油高进行转化，求得含参变量的体积公式，具有普遍适用性，不只是针对题目的问题，而是能解决一类问题。

缺点：

1、测量参数（油量、体积、变位程度等），其准确性主要与测量方法、容积表及参数修正系数密切相关，故本模型在一定程度上缺少了模型的综合误差量化估计。

2、任何量改变会对标定值造成不可估量的后果，故有必要考虑其他因素对标定值的影响, 如温度、压强、空气湿度等，而本模型中未考虑全面。

3、模型的建立是基于具体典型油罐体，而没有考虑到油罐体不均匀及地下油罐体所受到上面土壤等重力对它的影响。

4、本模型的建立也没有考虑到因地不同，地质不同，从而对应的地下油罐体要求不同等综合因素对实际罐体的作用。

6.2合理化建议

通过本模型的具体建立求解过程，我们主要在提高储油罐计量精度上以及定期对加油站的罐容表标定，提出了几点建议：

1）正确使用计量器具和设备，并在检定周期内使用；

2）定期对罐容表进行标定；

3）测量罐内的液位，油面稳定泡沫消失后才可测量，多次测量取平均值；

4）加油站人员要相对稳定，最好进行过培训，提高其安全意识和责任感。

爱华网本文地址 » http://www.413yy.cn/a/25101015/240327.html