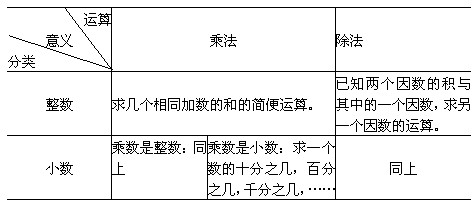
对乘法意义的理解
福建省诏安县白洋乡中心小学 吴幼盛
今天上午,中心校组织到塘西小学进行期初教学常规检查。我在检查沈长川老师的教学业务时,发现在学生的作业本中有一道填空题:“32个25相加的和可用算式____________来表示”。当学生填“32×25”时,他给予打“√”,而当有在学生填“25×32”时,他却给予判错。这种改法,倘若在以前毫无疑问是正确无误的,因为乘法的意义是“表示几个相同加数的和的简便运算”,其中规定表示“相同加数”的那个数必须写在乘号的前面,而表示“几个”的那个数必须写在乘号的后面。可如今的新课标对乘法意义的限定不是已经不再这么严格了吗,可以不用考虑两个因数的具体位置了?干嘛还非得强调学生必须把相同加数写在乘号的后面,而表示加数的个数写在乘号的前面呢?于是我便把这一看法提出来和他进行商榷。他听了我的意见,表示太确信我的说法,于是便请教一旁的许永辉副校长。许副校长说,列式时可以不用考虑因数的位置,但讨论意义时还是要强调因数的位置的,也就是说如果是“32个25是多少”列式时既可列成“25×32”,也可列成“32×25”,可反过来的话就不行了,即“25×32”只能表示“32个25是多少”而不能表示“25个32是多少”。
听了许副校长的解释,我觉得我这样理解还是有偏颇的。我记得曾在现行的二年级上册的数学教科书中的《乘法的初步认识》里的一段阐述:
3+3+3+3+3+3=18
像这样的加法,还可以用乘法表示,有()个3,用乘法算:6×3=18读作:6乘3等于18,或:3×6=18 读作:3乘6等于18。
这不就是说不管是“6×3”还是“3×6”都可以用来表示“6个3相加的和”吗?反过来当然也可以理解为“6个3相加的和”既可以用“6×3”来表示,也可以用“3×6”来表示。现在,怎么“25×32”就不能表示“25个32相加的和”呢?于是,我决定到电脑里查询一下,找出相关的理论依据来和他们进行探讨。可是,塘西小学的电脑根本上不了网。我便在自己的手机上查了起来,又发现手机里根本没有乘号可输入。这时,沈耀林老师也走过来参与讨论,他说:“如果两个因数都是整数的话,那以上两个算式都是可以的,可如果其中有一个因数是分数或小数,那就说不通了,比如6×就只能表示6的 是多少,难道它还能表示6个是多少吗?”我说,按照我之前看过的有关教参的意思就是两种说法都可以。他们三个一听,都坚决地摇头说:“不对不对!”
他们三位可都是中心校的数学权威,难道是我自己的理解错了?回到中心校,我马上上网查询了起来,发现网上大多数人的看法还都和他们一样,即主张对乘法意义的理解必须严格区分出两个因数的位置,不能混为一谈。我仍不死心,就找来了六年级数学上册的《教师教学用书》,看到其中对分数乘法意义的教材分析中有这么一段话:“因为现在不再区分乘数与被乘数,且学生已经学习过乘法交换律,所以整数乘分数的教学就可以归入分数乘整数的教学之中,所以本例只教学分数乘分数。分数乘整数的意义与整数乘法相同,且计算方法可由分数加法推导出来,学生较易理解”。可是,此时仅凭这段话似乎还是化解不了以上的困惑,无法说服他们同意我对乘法意义的理解。
吃完午饭,我无心和同事们喝茶聊天,继续在电脑里不停地翻啊找的,后来,我在百度上输入“分数乘法的意义”,然后把其中的解释条逐一地进行研读,发现虽然其中也有一些解读和我的理解是一样的,但那也只能代表部分网友的意见,还是没有找到足够可以支持我意见的有力凭证。我很不甘心,继续查找下去,此时,一条标题为“一、分数乘法意义的有关问题”的解释条映入我眼帘,我点开一看,发现链接到的竟然是“人民教育出版社课程教材研究所”的官方网站,这里可是全国最为权威的机构,这里的专家发表的解释意见绝对是全国最可靠的!我赶紧瞪大眼睛仔细地研读了起来,只见里面解释道:“掌握好分数乘法的意义,可为理解分数乘法的算理以及解决求一个数的几分之几的问题做好铺垫,故应加强对分数乘法意义的教学。教科书是把分数乘法的意义与算理结合在一起编排的,主要体现在例1和例3里。因为分数乘法的意义很重要,所以实际教学时可把意义和算理分开来讲,先把意义讲清楚,再结合意义来理解分数乘法的算理,就显得很自然,学生理解和掌握算理也更容易(可参见九义教材的做法)。”于是我继续研读下去,只见里面对“九义教材”是这么阐释的:“根据算式说意义与根据意义列算式的问题。这是现在讨论得比较多的一个问题。因为不再区分因数的位置,所以根据算式说意义就应分情况讨论。对分数与整数相乘来说,如×5,就有两层含义: (1)5个 2/3相加;(2)5的2/3。另一方面,根据意义列算式时,则可列出两个算式,但它们表示的意义都是特定的、唯一的。如根据5个2/3 相加列出乘法算式既可以是2/3×5,也可以是5×2/3 ,这两个算式在此处的意义是完全相同的,都表示5个2/3 相加,而不能说是5的 2/3。”
读到这里,我茅塞顿开:按照这里的说法,2/3 ×5的意义既可表示“5个 2/3相加”也可以表示“5的 2/3”;而“如根据5个2/3相加列出乘法算式既可以是 2/3×5,也可以是5×2/3”这不是和我的意思完全相符合吗?看来,我的理解没有错:现在,对于乘法意义的规定,已经不再像以前那样教条、机械了,即在a×b中,如果a和b都是整数,那么它既可以表示“a个b是多少”,也可以表示“b个a是多少”,而即便其中有一个因数b是分数或者小数,也可以不必去考虑整数因数到底在什么位置,都可以统一理解为“求a的几分之几是多少”或者是“求a个几分之几是多少”了。
当然如果是在特定的情境中,则算式所表示的意义还是是确定的,而不是两种理解都可以,比如在“把‘ 2/3+2/3 + 2/3+ 2/3+2/3’用乘法算式表示出来”这道题中,既可以写成“ 2/3×5”,也可以写成“5×2/3 ”,但此时两个算式的意义却只能是表示“5个2/3”而不能理解为“5的2/3”。相反,在“5瓶水可以喝3天,假设每天喝的水两样多,那么2天后喝了多少水”这问题中,列式时同样既可列为“5× 2/3”,也可列为“ 2/3×5”,可此时两个算式所表示的意义却都只能是“5的2/3是多少”,而不能是“表示5个 2/3是多少”。
 爱华网
爱华网