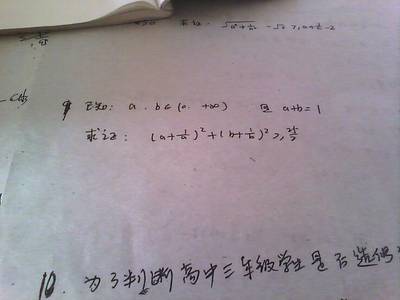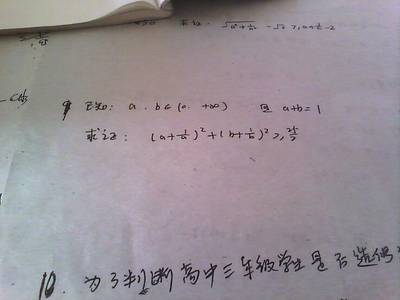不等式大师 绝对值不等式

Klamkin

Murray SeymourKlamkin先生一生著述颇丰，经历丰富。
　　　他生于1921纽约的Brooklyn，那儿他的父亲开着一家面包房，这是他一生喜好吃面包的明显原因。
　　　他的化工学士是1942年从Cooper Union工程学院拿的。二战期间他曾在马里兰化学武器部队服役。
　　　1947年，Murray获得纽约技术大学科学硕士学位并在那儿任教至1957年。此后加入了AVCO的研究与高级开发部。
　　　1962年，Murray短暂回归学术界，在SUNY，Buffalo当教授，后又成为Minnesota大学的客座教授．1965年，他挡不住工业界的诱惑参加福特汽车公司充当首席科学家直至1976年。
　　　在所有这些经历中，Murray渐渐成为数学问题解决的活跃分子。他的主要贡献是为SIAM（工业与应用数学学会）评论充当问题部分的编辑。因其介入了Putnam数学竞赛，故工作上与美国数学联合会关系密切。
　　　1972年MAA为组建参加1974年的国际数学奥林匹克参赛队做准备举办了美国数学奥林匹克竞赛。Murray无暇从福特公司获得空闲时间来训练队员，因此失望之余他另谋转换门庭。结果他来到加拿大，先是任Waterloo大学应用数学系的教授。但是不等Alberta大学的聘书寄到，他已决意离开。
　　　作为主席，Murray从私人工作环境中带来一种管理风格。显然并非每个人都愉快地接受它。但是他的确点燃了几把火，让一些人开始了研究的计划。
　　　Murray始终对欧几里得几何感兴趣。高中时代，他和朋友常常互相挑战几何尺规作图的各种问题。虽然当主席并没有教学职责，但Murray亲自上一个班的几何课。
　　　在此同时，Murray开始在上CruxMathematicorum编辑奥林匹克角，这本杂志那时是由Ottawa大学的LeoSauve私人出版。它现在成了加拿大数学会的官方杂志了。Murray还引入了本系的新生与大学生数学比赛。
　　　Murray一直是美国IMO1975年以来的副领队。1981，美国成为这项赛事的主办者，第一次在欧洲以外的地区召开。通常的领导人SamGreitzer，成为了主要组织者。Murray接替了这个领导职位。
　　　1982年我第一次去了欧洲，因为那年的IMO在布达佩斯举行。后来的一届1983后在巴黎，1984届在布拉格。我发现与会者因Murray的出席深感荣幸。他是一个全世界有争议的最知名的数学问题解决家。
　　　他的主席的头衔也在1981年到期。他和他的妻子Irene没有孩子，他们很好客。
　　 他是个商业气息很浓的人，他的天赋闪耀在他真知灼见的观点和手到擒开的高效上。
　　　尽管Murray在每样他尝试做过的事情上都成功了，但他最终可能会被记住的最重要的事是他参与了数学问题解决和竞赛。他创作或主编了四本问题书，在每一个有问题求解的核心的数学刊物是留下了印记。他接受过滑铁卢大学的荣誉博士学位又是瑞士皇家学会的会员。他荣膺无数的奖，某些奖的名称也以他的名字命名。
　　　　Murray的漫长的一生健康状况良好。直到2000年才有了些不太妙的情况，那年九月他接受一次搭桥的手术。当他出院后他继续努力步行上班，登六楼台阶到办公室。

　　　他的逝世也许会是数学竞赛和问题解决的时代的结束的标志，人们会深深怀念他。http://cms.math.ca/crux/v27/n2/CRUXv27n2.pdf

1982年美国数学杰出贡献奖的得主是数学界一位大名鼎鼎的人物---几十年来一直活跃于科研、教学、写作和一些学术组织的开拓性工作的埃德温·福特·贝肯巴赫（Edwin FordBackenbach）教授。同年9月5日，他便与世长辞，但他的巨大影响巳经广为人知并将经久不衰。
埃德温1906 年出生于美国Texas州 Dallas 市 ，他在那儿上了学并一直念完高中。1924年秋，他进了Houston 的Rice 学院（现为Rice大学），并于1931 年获得哲学博士学位。大萧条的1931年，寻找职业实非易事，但埃德温在三十年代的这段艰难岁月里却干得相当出色。他在Princeton 、 Ohio 和Chicago做了两年国立研究员。1933 年，他回Rice学院任职；1940 年，他到Michigan 大学当了两年助理教授，1942年，他又去Texas大学，当了三年副教授。自1945 年起，他在California 大学Los Angeles分校当了三十多年的数学教授。
埃德温的博士论文是关于极小曲面的研究。由于极小曲面的距离函数与面积变形函数的对数都是次调和函数，埃德温陷入了关于次调和函数的大量不等式之中；这激发了他对一般不等式的毕生兴趣。60年代起，埃德温沉醉于不等式的研究与写作之中……。他的75 篇研究论文大都发表在美国的主要刊物上。

在埃德温1945 年去California 州立大学前，LosAngeles分校的数学系远没有现在这样高的地位。该校的第一个数学博士出自埃德温门下，1947 -1920 的24年间，他共带了十名哲学博士。学生们都对他有着美好的记忆：“他十分平易近人，与学生相处融洽。他说话很中听，从不因发怒而尖刻地挖苦。他对待我或其他学生的方式，用‘朋友‘一词来形容是再恰当不过的……从某种意义上讲，他是个很好的论文指导者：当我误入迷津时，他及时给予指点；当我仅需进行钻研时，他便独自离去。”

埃德温著述甚广，他曾和理查德· 贝尔曼（Rchard Bellman）合写了两本有关不等式的书：《 不等式入门》（1961 ）（被收进美国数学会的新数学丛书中），《不等式》 ( 1961）（拓展了哈代、李特伍德和波利亚的《不等式》的方法和课题的范围，成为一本标准的参考书），他还是数学大辞典的编辑之一。除了这些高级工作外，埃德温还是一个科普作家，他与别人合写了一系列具有初等、中等和高等水平的读物。他还为中学数学研究会、美国数学教师协会和非洲教育计划写过文章。在写作和编辑之余，埃德温把时间和精力都倾注在一些学术机构上，这其中当然包括美国数学协会。

埃德温是美国数 学会的成员，当美国《数学评论》一度处于不景气状态时，他曾担任过一个与此有关的特别委员会主席来负责此事。他还是“国际一般不等式会议”的组织者之一。

上面只介绍了埃德温为世界数学事业做出的不胜枚举的贡献中的几个范例。尽管如此．如果不提及他在《太平洋数学杂志》中所起的巨大作用，那么任何一篇介绍都将是不够全面的。这家杂志的1982年第1 期的刊首语，就是献给创办该杂志的最杰出的两位奠基人：埃德温·福特·贝肯巴赫与Berkely 大学的弗兰提塞克· 沃尔夫（Frant 1 sekWolf）。对于常人来讲，创办一种刊物巳非易事，至于那些有足够的洞察力与精力，同时对两种刊物都做出重大贡献的人更是凤毛麟角，而埃德温就是这样一个出类拔萃的人。他在1946---1951 的五年间，担任了《美国数学月刊》的通讯编辑，主持“数学短文栏”。1971年后，他一直担任美国数学协会出版委员会的主席，并以极大的热情、充沛的精力和高超的技巧来指导这些杂志、丛书和论文的问世。
在所有的活动中，埃德温以他出色的谈判技巧、一贯地彬彬有礼和对他人诚挚的关心、以及渊博的学识和恰到好处的幽默，赢得了许多同事的合作。但在其它活动中，他在会议桌上所表现出的那种合作与通融精神消失殆尽：在网球场上，他是一个凶悍的人物，一个从不给对方以喘息之机的强硬对手。三十年代，他曾是Rice大学的网球冠军，后来又当了教练。整整六十年间，他对这项最喜爱的运动总是爱不释手，就是在去世前不久，他还与妻子参加了美国的超级大赛。

樊畿

樊畿， KyFan，1914年9月19日生于浙江杭州，初中阶段先后在金华中学、杭州宗文中学和温州中学就读．他各科成绩均优，唯不喜欢英文，原因是“讨厌呆板地记忆生词和不可理喻的文法”．　1932年秋，樊入北京大学数学系．他本想读工科，但因姑父冯祖荀在北京大学任数学系主任，更由于北大不考英文，因此决定樊走上了数学道路．樊攻读数学得心应手．　　

1936年，樊在北京大学毕业之后，留校任教．1938年下半年，由法国退回庚子赔款设立的中法教育基金会，招考数学、化学、生物三科各一名去法国留学．樊是数学科的被录取者．1939年初启程去巴黎．他本打算攻读代数学，但在临行前，程毓淮和蒋硕民两教授建议他跟随M．R．弗雷歇学习，指出“弗雷歇的分析和代数差不多”．对这一指点，樊终生感激．确实，作为泛函分析先驱学者的弗雷歇，曾发展一套抽象的分析结构，在当时崇尚函数论等“硬分析”的法国独树一帜．樊到巴黎之后，请曾来中国访问的J．阿达玛给弗雷歇写了一封介绍信，彼此渐渐熟悉，弗雷歇就成了樊的导师．

1941年，樊以“一般分析的几个基本概念”的学位论文，获得法国国家博士学位．当时第二次世界大战正在进行，樊幸运地成为法国国家科学研究中心的研究人员，并且在庞加莱数学研究所从事数学研究．战时的生活紧张而清苦，但研究工作不断取得成果．樊在第二次世界大战之后，转往美国发展．1945—1947两年，他是普林斯顿高级研究院的成员．当时，世界著名数学家云集普林斯顿，其中包括战前已来美国的H．外尔和J．冯·诺依曼．樊后来的工作深受他们的影响，学术上也有更大的进展．

1947年之后，樊去圣母大学任教，从助教授、副教授，到教授．1960年曾到底特律城的韦恩州立大学任教一年，随即转到芝加哥附近的西北大学，直至1965年应聘为加州大学圣巴巴拉分校数学教授．

1964年，台北中央研究院推选樊为院士．1978—1984年1745间，他曾连任两届该院的数学研究所所长．从1960年起，担任《数学分析及其应用》的编辑委员共32年．他还是《线性代数及其应用》的杰出编辑，1993年又被聘为荷兰的《集值分析》和波兰的《非线性分析中的拓扑方法》的编辑委员．

1985年夏樊正式退休．数学界为他举行了盛大的学术活动，世界各地的许多数学家前来参加．

1989年5月，樊应北京师范大学之邀回到阔别50多年的北京，讲学两周之后，又去北京大学、中国科学院数学研究所、武汉大学、浙江大学、杭州大学等校演讲．访问期间被聘为北京大学和北京师范大学的名誉教授．　

樊的学术成就是多方面的．从线性分析到非线性分析，从有限维空间到无限维空间，从纯粹数学到应用数学，都留下了他的科学业绩．以樊的名字命名的定理、引理、等式和不等式，常见于各种数学文献．他在非线性分析、不动点理论、凸分析、集值分析、数理经济学、对策论、线性算子理论及矩阵论等方面的贡献，已成为许多当代论著的出发点和一些分支的基石．

樊做学问和上课同样认真，从不浪费一分一秒．黑板上的字也是一字不多一字不少．他还有许多一流的讲义，可惜他不肯发表．

樊能说多种语言．但他自嘲说：“我的英文中有法国口音，讲法文时有德国口音，而讲德语时则有中国口音．”他说他学外语的目的只是为了看数学书，所以不大注意发音．

樊待人宽厚，助人为乐．他常说：“为人作事，必须对别人有帮助，自己才会快乐．”最终解决比贝尔巴赫猜想的L．德·勃兰治，在成名前曾受冷落，而樊一直对他热情鼓励，他的许多论文都经樊推荐而发表．

樊和夫人燕又芬住在美国加州圣巴巴拉的一座小山上，山下是大海，风景如画．在回首往事时，樊一直牵记着引导他走上数学道路的冯祖荀先生．

Hayashi

     廿世纪初叶最重要的日本数学家有林鹤一（Tsuruichi Hayashi,1873-1935）和高木贞治（Teiji Takagi,1875-1960）.

    林鹤一创办了东北帝国大学的数学系,并用自己的收入创办了Tohoku数学杂志.

     日本文部省設立高等學校時（明治十九年），用一、二、三、四…命名，一共有五所，後來增為八所。例如，一高在東京，二高在仙台，三高在京都，四高在金澤。以歷史而言，當然是三高的歷史最悠久。事實上，三高出了不少有名的人物。文科方面不提，日本有五個理科的諾貝爾獎得主，湯川秀樹、朝永振一郎、江崎玲於奈、福井謙一、利根川進。其中，湯川、朝永、江崎都是出身三高；除了江崎之外，其餘四人都是京都大學畢業的；並且，湯川與福井後來都在京都大學任教。以數學界來說，東京帝大的高木貞治、吉江琢兒、掛谷宗一，京都帝大的園正造、岡潔、秋月康夫（Y. Akizuki），東北帝大的林鶴一（T. Hayashi）、藤原松三郎(M. Fujiwara, 1881－1946)，全是出身三高的。林鶴一與藤原松三郎是《東北數學雜誌》（Tohoku Journal of Mathematics）的開創者。

     对高木影响最大的老师乃是第三高中时代的数学先生河合十太郎(KawaiJiutar)，正是由于河合的影响，促使高木选择了以数学研究为毕生的职业．河合的学生中有林鹤一、吉江琢兒、藤原松三郎等人，他们后来都成了本世纪上半叶日本著名的数学家．在第三高中，吉江与高木（1891年进入第三高中）同班，而林则高一班．

     東北帝大(1910 年成立)成立不久, 數學教授有林鶴一、藤原松三郎与窪田忠彥 (Tadahiko Kubota, 1885－1952)。 藤原與窪田分別是陳建功和苏步青的老师。苏步青教授和陈建功教授都是在东北大学获得的博士学位。  

GARFUNKEL

One of Crux's regularcontributors since its earliest days, Jack Garfunkel, passed awayon New Year's Eve, 1990. His many proposals in geometry, sometimesvery dicult,but often beautiful, were well appreciated by Cruxreaders. He will be missed. The following information on his lifewas kindly furnished by his son, Sol Garfunkel.Jack was born inPoland in 1910 and came to the United States at the age ofnine.Although one of the top math majors at City College inNew York, he left academic life after graduation to help his familyweather the depression. For the next 25 years, he workedmanufacturing candy. At the age of 45, he returned to his firstlove and became a high school mathematics teacher. Over the next 24years, he taught at Forest Hills High School, supervising over twodozen Westinghouse finalist and semi-finalist winners of the talentsearch. When he "retired"from high school teaching, he immediatelybegan work as an adjunct professor at Queens College and later atQueensborough Community College,where he taught until November of1990.Throughout his two careers as candyman and teacher, hecontinued to do mathematics,conjecturing and solving problems insynthetic geometry and geometric inequalities.While his formaleducation ended with his undergraduate work, he never lost hiscuriosity and love of his subject.

博主正在阅读的《数学天书中的证明》（第四版）（高等教育出版社2011年版）中有不少数学大师的照片，下面的三张应该不多见。

波利亚（George Polya，1887-1985），1924年在G． H． 哈代(Hardy)的推荐下，波利亚去英国逗留了一年，先后访问牛津大学、剑桥大学等著名高等学府.在此期间参加了由哈代与J． E． E． 李特尔伍德(Littlewood)主持的经典著作《不等式》(Inequalities)的写作。

李特尔伍德（Littlewood John Edensor，1885～1977），20世纪20年代后期，李特尔伍德从幂级数的均值和有界双线性形式两个方向研究了不等式。1934年，他与哈代、G．波利亚(Pólya)合作出版《不等式(Inequalities)一书，这是不等式方面的第一部专著。李特尔伍德与哈代之间几十年的合作是默契而成果丰硕的。通常，李特尔伍德将文章的基本框架搭好，使用那些哈代熟悉的符号进行表述，然后由哈代补充完善成为一篇形式优美、内容严谨充实的论文。李特尔伍德和G.H.哈代一道在20世纪上半叶建立了英国的具有世界水平的分析学派。

在数学写作上，柯西Cauchy,Augustin-Louis,1789－1857）被认为在数量上仅次于欧拉的人。柯西不等式是由柯西(Cauchy)在研究数学分析中的“流数”问题时得到的。但从历史的角度讲，该不等式应当称为Cauchy-Buniakowsky-Schwarz不等式，因为，正是后两位数学家彼此独立地在积分学中推而广之，才将这一不等式应用到近乎完善的地步。柯西不等式非常重要，灵活巧妙地应用它，可以使一些较为困难的问题迎刃而解。

本书介绍了40个著名数学问题的极富创造性和独具匠心的证明。其中有些证明不仅想法奇特、构思精巧，作为一个整体更是天衣无缝。难怪，西方有些虔诚的数学家将这类杰作比喻为上帝的创造。

本书的英文原著第一版于1998年出版。

第1章 素数无限的六种证明
第4章 表自然数为平方和
第17章 集合，函数，以及连续统假设 　　
第18章 不等式颂

一个不等式大师的自白

爱华网本文地址 » http://www.413yy.cn/a/25101014/235526.html