前面考察了一个应力集中的问题。算例表明,当台肩处没有倒角时,在台肩处存在应力集中,且用有限元无法得到真实的--应力解。
这里再考察一个类似的例子如下图。该结构左边固定,而在下面直线上施加竖直向下的分布力系,现在逐渐加密网格,考察台肩处应力值的改变。
(1)使用5mm的单元尺寸对该面进行网格划分
得到的有限元模型如下
计算结束后,绘制该面的米塞斯应力云图如下,此时,固定端的上下边沿显现出最大值。
(2)使用2mm的单元尺寸对该面进行网格划分
得到的有限元模型如下
计算结束后,绘制该面的米塞斯应力云图如下,此时,固定端的上下边沿显现出最大值,但应力值上升。
(3)使用1mm的单元尺寸对该面进行网格划分
得到的有限元模型如下
计算结束后,绘制该面的米塞斯应力云图如下,此时,应力最大值点已经转移到台肩处,应力大幅度增加。
(4)继续使用1mm的单元尺寸对该面进行网格划分,但是对上述应力最大值点局部加密网格。
得到的有限元模型如下
计算结束后,绘制该面的米塞斯应力云图如下,此时,应力最大值点仍旧在台肩处,应力暴增。
(5)继续使用1mm的单元尺寸对该面进行网格划分,但是对上述应力最大值点局部加密网格第二次。
得到的有限元模型如下
计算结束后,绘制该面的米塞斯应力云图如下,此时,应力最大值点仍旧在台肩处,应力继续暴增。
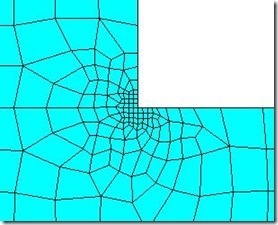
5)继续使用1mm的单元尺寸对该面进行网格划分,但是对上述应力最大值点局部加密网格第三次。
得到的有限元模型如下
计算结束后,绘制该面的米塞斯应力云图如下,此时,应力最大值点仍旧在台肩处,应力以几倍的速度上升,结果已经毫无意义。
【评论】
 爱华网
爱华网