源地址:http://class.htu.cn/xljytj/02/022.html
第二节 中数
一、中位数的概念
二、中位数的计算方法
三、中数优缺点
四、中位数的适用条件
五、百分位数的概念及其计算方法
一、中位数的概念
中位数,又称中数、中点数,符号Md(Median)。是指位于一组数据中较大一半与较小一半中间位置的那个数。即它位于依一定顺序排列的一组数据中央位置的数值,在这一数值上、下各有一半频数分布着。这个数可能是数据中的某一个,也可能根本不是原有的数据。
中位数是把按从小到大(或从大到小)排列的一组数据一分为二的数据,是位于一组数据中较大一半与较一半中间位置的那个数,它将整个数据的个数分作大的一半和小的一半,而不是将数据的值分作相等的两部分。
它是集中量的一种指标,是百分位数的一种。中位数可能是数据中的某一个,也可能根本不是原有数据的数。
中位数(概念要点)
集中趋势的测度值之一
排序后处于中间位置上的值
不受极端值的影响
主要用于定序数据,也可用数值型数据,但不能用于定类数据
各变量值与中位数的离差绝对值之和最小,即
二、中位数的计算方法
1.用原始数据计算法--未分组数据求中数的方法
根据中位数的概念,首先将一组原始数据依大小顺序排列后,然后找出位于中间的那个数,这里又分两种不同的情况:
1)单列数目的情况――-即不重复数据
所谓单列数目是指一组数据中没有相同的,这时取处于中间位置的那个数为中位数:
若总频数为奇数,则位于中央的数据,即取序列中第(N+1)/2的那个数为中位数;
若总频数为偶数,则以最中间两个数据的算术平均数作为中位数,即取序列中第N/2和N/2+1个这两个数据的均数为中数。
从中位数的概念及计算中可以看出,求中位数不受极大值与极小值的影响,而决定中位数的是居中的那儿个数据的数值大小。
2)一组数据中有重复数值的情况:
所谓有重复数目是指一组数据中有数值相同的数。这时计算中位数的方法基本同单列数目,但当位于中间的那几个数是重复数目时,求中位数的方法就比较复杂了。具体算法如下:
当重复数值没有位于数列中间时,方法同上。
当重复数值位于数列中间,则将重复的数据视做连续数,将它细分为n个数,此后的计算与上同。
如数据:2、3、5、5、7、7、7、11、13,居中的数是7,但7是重复数,这是要将7视作连续数。N/2是4.5,序列中上下各4.5的那一点恰和是第一个7的中点,而这人7的中点如何确定呢?我们知道将7视作连续数可以理解为6.5――7.5之间有三个数据分布其中,而这三个7是均匀分布在这区间之内的,如图所示:
6.5――7.5之间均匀分布三个数据,每一个数据占1/3的距离,那么可理解为第一个7落在6.5-6.83这一区间内,第二个7落在6.83-7.16这一区间内,第三个7落在7.16-7.5区间内。第一个7的中点是6.67,这一点就是整个序列中位居最中间的那一点,因此,该组数据的中数是6.67。这是重复数列为奇数的情形。
如果是偶数,作法也同奇数基本相同。如在上组数据后面再加一个15,它就成偶数重复序列了。数据为:2、3、5、5、7、7、7、11、13、15,此时N/2等于5,那就是说该组数据的中点应该是第5个数的上限,第6个数的下限,如上图所示,第一个7的上限为6.83,即该组数据的中位数为6.83。
上面的计算方法比较复杂,其它统计书中大多没有这样严格划分,SPSS程序中也没有这个计算,我们能理解其实质就可以了,通常计算时,大多是按照定义进行。
中位数(位置的确定)
未分组数据的中位数(计算公式)
定序数据的中位数(算例)
未分组数据的中位数(计算公式)
数值型未分组数据的中位数 (5个数据的算例)
数值型未分组数据的中位数 (6个数据的算例)
2.已分组数据(频数分布表)求中数的方法
若原始数据已经整理成了次数分布表后,求中位数的原理同重复数目求中位数是一样的,即可以用内插法计算,也就是取序列中将N平分为两半的那一点的值作为中位数。
基本原理同有重复数值位于数列中间的情况
即取序列中将N平分为两半的那一点的数的值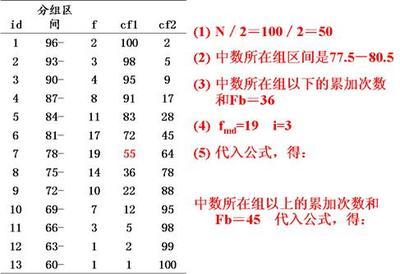
次数分布表求中位数的具体步骤如下:
求N/2,并找到N/2所在的分组区间;
求含有中位数那一区间以下各区间的次数和,即中位数所在组区间下限以下的累加次数。记作Fb(或n1,见王P38);
求N/2与Fb之差;
求序列为第N/2那一点的值。
设中位数所在那一组的区间的数据次数为fMd,Lb为中位数所在那一分组区间精确下限值。
根据重复数列求中位数的原理,设有fMd的数据均匀地落在距离为i的区间内,那么每个数据各占i/fMd,那么至N/2这一段距离为i/fMd×(N/2-Fb.
求中位数的公式如下:
由数值小向数值大的方向计算(即用精确下限计算)时,
同理,由数值大向数值小的方向计算(即用精确上限计算)时,
上面公式的含义为:
Fb:含有中数那一组以下的各个组的次数之和
Fa:含有中数那一组以上的各个组的次数之和
Lb:中数所在组的下限;
La:中数所在组的上限;
fmd:为中数所在组的次数;
i: 代表组距。
数值型分组数据的中位数(算例)
【例】根据表中的数据,计算50 名工人日加工零件数的中位数
例
计算中位数案例
3.利用曲线图
累加曲线图
频数分布图
三、中数优缺点
1、中位数的优点:
从中位数的的计算可以看出:
中位数是根据观测数据计算而来,不能凭主观臆定。可用中位数作为数据集中趋势的指标。
计算简单,容易理。中位数的概念简单明白。
很少受两极端数值的影响。
2、中位数的缺点:
反应不够灵敏,两极端数目变化,对中位数不产生影响;
计算中位数时,不是每个数据都加入计算,受抽样的影响较大,不如平均数稳定;
中位数乘以总数与数据的总和不相等(只有少为情况,即当中位数等于平均数是时相等);
中位数不能作进一步的代数运算。
四、中位数的适用条件:
(1)当一组观测结果中出现两极端数值时。
这种情况在心理与教育科研实验中常常出现,因为心理与教育实验中的偶然因素非常复杂,有时实验中为了平衡各各误差,经常是同一种观测要在同一个被试身上反复进行多次,而只取某一个代表值作为对该被试的观测结果,这时若出现两极端数目,又不能确定这些极端数目是否由错误观测造成,因而不能随意舍去,在这种情况下,只能用中位数作为该被试的代表值,这样做,并不影响进一步的统计分析。
(2)当一组数据的两端或个别数据不清楚时,只能取中位数作为集中趋势的代表值。
在心理与教育实验中,经常会出现个别被试不能坚持继续进行实验这一现象,有时只知个别被试的观测结果是在分布的哪一端,但具体数值不清楚,这种情况下,就只能取中位数,而不能计算平均数。
(3)资料属于等级性质时。
(4)当需要快速估计一组数据的代表值时,也常用中位数。
五、百分位数的概念及其计算方法
1、百分位数的概念
百分是位于按一定顺序排列的一组数据中某一百分位置的数值。一般用Pp表示。
如第70百分位数(P70),就是在按从小到大排列的一组数据中小于这数值有70%个频数,大于这个数值有30%个频数的那个数值。中位数就是第50百分位数。小于它有50%个频数,大于它也有50%个频数。它是百分位数中的特例。
在教育与心理测量中,常通过计算某个原始分数的百分位数来说明、解释、评价它在团体中所处的位置。
2、百分位数的计算方法
在频数分布表上可以用内插法计算某个百分位数。
其计算公式为:
其中:Pp 表示百分位数
p 表示与百分位数相对应的比数
N 表示总频数
Lp 表示百分位数所在组的下限
n 表示小于百分位数所在组下限的频数总和
fp 表示百分位数所在组的频数
i 表示组距
 爱华网
爱华网