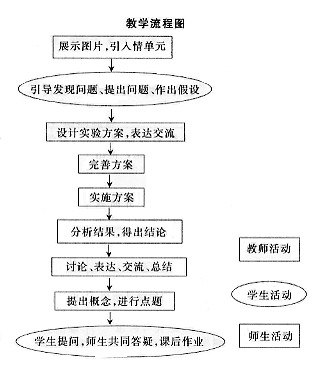
实验三动平衡实验
一、实验目的
1.掌握刚性转子动平衡的实验方法及使用的设备仪器;
2.验证动不平衡和动平衡的概念。
二、实验仪器设备及用具
1.单点动平衡机
2.磁电式传感器CD-4型
3.测振仪GZ-1型
4.自备:计算器、量角器、铅笔、尺
三、实验内容
1.刚性转子的动平衡实验
2.在刚性转子的不同回转面上进行平衡实验并比较
四、动平衡实验的工作原理及单支点动平衡试验机
转子的动平衡实验一般在动平衡试验机上进行。动平衡试验机是用来检验和校正刚性转子的不平衡量的大小和相角位置的设备。其基本原理是:当待平衡的转子高速回转时,由于质量分布不平衡,产生的离心惯性力的作用而振动,测定所产生的振动或利用补偿质径积以消除振动,从而求出其不平衡量的大小和方位。
动平衡实验机的种类很多。常见的动平衡试验机大致由三大部分组成:使被支撑转子以一定转速回转的驱动部分;支撑被试转子的左右两个弹性支撑架;检测不平衡振动并由此指示转子校正平面内不平衡量大小及相位的电测部分。
1.单支点平衡试验机及实验原理
单支点平衡试验机的结构简图如图一所示。被试转子为1;皮带3由电动机驱动,皮带3靠摩擦使转子3回转,组成驱动部分;弹簧6和框架2组成弹性支撑架(注意是单固定支点);传感器4和测振仪5组成电测部分。
1.被测转子 2.框架3.驱动皮带 4.传感器5.测振仪 6.弹簧
图一 单支点动平衡实验机简图
当转子转动时,其上的不平衡质量产生的离心惯性力作用到弹性支架上,使框架2绕支点摆动,摆角为θ,形成一不平衡激振型的振动系统。当转子被驱动的初始转速高于框架的固有频率时,立即停止驱动。转子由于轴承的摩擦和空气的阻力作用,转速ω逐渐降低,当框架系统的振动频率接近其固有频率ω0时,进入共振区,振幅逐渐增大,在ω=ω0时产生共振,振幅达到最大值。
由于转子的两个选定平面中的一个(工作面)通过支撑点,因此该平衡平面上的等效惯性力对振动系统不起作用。由此可知,振动系统只受另一个待平衡面(Ⅱ)上的等效惯性力的作用。
根据不平衡激振原理,框架的瞬时角振幅θ为
式中:λ为频率比,λ=ω/ω0;

ω为不平衡激振频率(即转子的角速度);
ω0为振动系统固有频率;
J为振动系统绕支点摆动的转动惯量;
m 为待平衡面上选定半径上的等效不平衡质量;
R 为待平衡面上的选定半径;
L 为待平衡面到支点的距离;
ζ 为阻尼率;
φ 为相位角。
共振时λ=1,振动系统的最大角振幅和相位角为:
θ=m RL/2Jζ
φ=90?/FONT>
由于J和L是与结构有关的参数,对于一个具体的振动系统和待平衡的转子来说,二者均为常数(该实验装置J=,L=mm),从上述可以看出,共振时其振幅与mR成正比,且此时的不平衡质量的相位超前振幅90海谑牵捎貌饬靠蚣苷穹姆椒浣拥胤从吵鲎拥牟黄胶饬俊?/FONT>
但是,由电测仪器测得的是框架摆动的线位移x,它与框架角振幅θ的关系为:x=θl=mRLl/2Jζ=GRLl/2Jgζ=KGR
式中:l为测量点到支点的距离;
g 为重力加速度;
K=Ll/2Jgζ为比例常数;
GR 为重径积。
因此,可通过实验求得K和GR的数值,并找到不平衡量所在的相位。
2.电测部分的基本工作原理
为求得转子的不平衡量,需要测量并显示出一个校正平面上的不平衡量的大小和相位角。
现代动平衡试验机的测量显示部分几乎均采用电子技术
(1)传感器
传感器的作用是将振动系统的振动变换成电信号,传感器的测量杆与振动系统的摆杆刚性连接为一体,测量杆与敏感线圈连接。摆杆振动时带动敏感线圈在磁场中作切割磁力线运动,在敏感线圈两端产生与振动速度成正比的感应电动势。
CD-4传感器如图二频率范围0~300HZ,最大可测位移15mm,动圈阻抗约30KΩ,运动部分重量约28克。
图二CD-4传感器
(2)测振仪—测量指示装置如图三
测振仪的作用是传感器输入的电信号---电动势,经过模拟解算电路输入放大级、滤波,然后将转子的不平衡量的数值和相位显示出来。
图三 CZ-1测振仪
GZ-1测振仪将CD-4传感器输入的电信号,经积分电路后变成正比于振动位移或加速度的电信号,通过电压表显示数值;测量选择——V代表速度,a代表加速度,x代表位移,f0代表测振仪固有频率(f0=2.5HZ)。
工作选择——1表示阻尼小,2表示阻尼大。
量程——10μ档读表盘上刻度0~10,30μ档读表盘上刻度0~30,100μ档读表盘上刻度读数乘以10,就是实测得的位移数值。
五、测量方法
1.测振仪
(1)转子不加任何重量时,测得最大振幅A如图四(a)所示,A是由所选定平衡面上的等效重径积产生的。
(2)在选定半径的任意方向加已知重量为Q的磁铁块,测得最大的振幅B如图四(b)
(3)将磁铁块Q取下加在原位置的反方向对称位置上,即180捍Γ獾米畲笳穹缤妓模╟)。
图四
设由磁铁块Q本身产生的振幅为D,则振幅A、B、C、D之间的向量关系为:
在图4-4(d)中,△acd可求得
cosα=(A2+D2-C2)/2AD
又在△adb中可求得
cos(180?α)=(A2+D2-B2)/2AD
cosα=-cos(180?α)
所以A2+D2-C2=-(A2+D2-B2)=-A2-D2+B2
有:D2=(B2+C2-2A2)/2
KGR=A
KQR=D
得到:K=DR/Q
G=AQ/D
由于加重磁铁块Q和位置是已知的,所以不平衡重量与其相位角α可求出。为了方便取B、C振幅中的较小者的加重处为参考位置,图4-2中C<B。所以选C为参考位置处的振幅,则有
α=cos-1[(A2+D2-C2)/2AD]
六、实验步骤
1.第一次动平衡实验
(1)将测振仪两旋扭分别放在x(f>1)档和1档,量程开关置于30μ档;
(2)按下手柄驱动转子,体会一下共振值;
(3)测量出振幅A、B、C;
(4)计算G、α;
(5)用天平称出G,按α角加在转子上(这时Q应取下),选择振幅中B、C较小者为基准位置,顺时针按α角处加G试,振幅明显减小位置时位置正确,否则逆时针按α角处加G观察平衡。
(6)第一次动平衡试验平衡精度在5μ以内(偏心距)。
2.在不同回转面上进行动平衡比较
实现刚性转子的动平衡,可在刚性转子上任意选择两个回转平面,但是两个回转平面间的距离远些比近些其平衡重量小。
(1)将第一次所加的平衡重量全部取下,选ⅡⅢ作为平衡回转面重复作,计算出G2、G3,GL=G2L2=G3L3;
(2)称出G2或G3,加在平衡回转面上,观察是否平衡。
图五 转子尺寸图
3.注意事项
若测得的数据误差太大,在计算D时根号内可能出现负值,或计算α角时超出值域,则测得数据无效,须重测,所以操作方法必须正确。
(1)皮带手柄下压时不得过猛,引起框架振动;用手托住手柄,压力不要太大,防止掉皮带;
(2)测试不得晃动工作台;
(3)不要加速时的共振值,而要取停止加速后转子减速到其振区时的共振值;
(4)正面读表盘上的数值;
(5)每次装取磁铁块时,应将测振仪关上,防止表针打弯;
(6)配重块弧面不要反装。
七、思考题
1.哪些类型的构件需要平衡实验?平衡的条件是什么?
2.为什么在动平衡试验时要使一个平衡回转面通过框架的振摆轴线?当试件的一个平衡回转面已经平衡后,要平衡第二个平衡回转面时是否仍需使第一个平衡回转面通过框架的振摆轴线?
3.为什么要使平衡框架构成的振动系统在共振时测量试件的不平衡重量?怎样可使一个振动系统共振?
4.动平衡机进行动平衡实验的原理是什么?
 爱华网
爱华网