我用了两年时间系统详细研究三角形,先后证明三角形三条角平分线交于一点(内心)、三边垂直平分线交于一点(外心)、三条中线交于一点(重心)、三条高交于一点(垂心)。证明这些,最终是要为今天证明的这个命题做铺垫的。如果我都不能证有重心、垂心、外心之类,又怎样证三者的共线?
已知:△ABC中,P为其垂心,O为其重心,Q为其外心。
求证:P、O、Q共线且OP=2OQ
证明
作BC的中点D、AC的中点E,连接并延长AP交BC于F,连接并延长BP交AC于G,连接AD、DE、DQ、EQ
∵Q为△ABC外心(已知),D、E分别为BC、AC中点
∴DQ为BC垂直平分线,EQ为AC垂直平分线(外心为三角形任两边垂直平分线交点)
∴DQ⊥BC,EQ⊥AC(垂直平分线定义)
∵P为△ABC垂心(已知)
∴AP⊥BC,BP⊥AC(垂心为三角形任两高交点)
∴AP∥DQ,BP∥EQ(垂直于同一直线的两直线平行)
∵D为BC中点,E为AC中点(由辅助线做法)
∴AB∥DE,且AB/DE=2(三角形中位线平行于第三边且等于此边一半)
∴△ABP∽△DEQ(三边分别对应平行的两三角形相似)
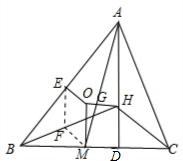
∴AP/DQ=AB/DE=2(相似三角形对应边成比例)
∵O为△ABC重心(已知),AD为BC上中线(辅助线做法)
∴O在AD上且AD/OD=3(重心是三角形任一中线靠近边一侧的三等分点)
∴OA/OD=2(比例代换)
∵AP∥DQ(已证)
∴∠PAO=∠QDO(两直线平行,内错角相等)
又∵AP/DQ=OA/OD=2(等量代换)
∴△AOP∽△DOQ(两边对应成比例且其夹角相等的两三角形相似)
∴OP/OQ=OA/OD=2,∠AOP=∠DOQ(相似三角形对应边成比例,对应角相等)
∵A、O、D共线(已证)
∴∠AOQ+∠DOQ=180°(顺序共线三点成平角)
∴∠AOQ+∠AOP=180°(代入)
∴P、O、Q三点共线(平角两边上点与顶点共线)
证明完毕
三角形重心、垂心、外心共线,且重心到垂心距离等于重心到外心距离的两倍。此线称为欧拉线。
 爱华网
爱华网