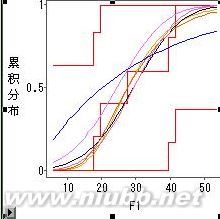
=|c|^2+2-2sqrt(2)|c|cos<c,a+b>=1
即:cos<c,a+b>=(|c|^2+1)/(2sqrt(2)|c|)∈[-1,1]
(|c|^2+1)/(2sqrt(2)|c|)≤1,可得:sqrt(2)-1≤|c|≤sqrt(2)+1
(|c|^2+1)/(2sqrt(2)|c|)≥-1自动满足,不用解
故|c|的最大值:sqrt(2)+1
----------------------------------
当然也可以用数形结合的方法:
在单位圆上任意找2个垂直向量,画出他们的和,即正方形的对角线
以正方形的对角线的终点为圆心再画一个半径为1的圆
则c在此圆上运动,当c与正方形的对角线同向时,|c|最大,为:sqrt(2)+1*************************a=(1.0)
b=(0,1)
设c=(x,y)

c-a-b=(x-1,y-2)
(c-a-b)^2=(x-1)^2+(y-1)^2=1
x-1=cosθ
y-1=sinθ
x^2+y^2=(1+cosθ)^2+(1+sinθ)^2=3+2(sinθ+cosθ)
=3+2√2sin(θ+π/4)
(x^2+y^2)max=3+2√2=(√2+1)^2
(x^2+y^2)min=3-2√2=(√2-1)^2
|c|=√(x^2+y^2)
|c|max=√2+1
|c|min=√2-1**********************************已知ab是单位向量,a×b=0,若向量c满足c-a-b的绝对值等于1,则c的绝对值得最大值是多少?
数形结合:a、b是相互垂直的单位向量,故在单位圆上任意找2个垂直向量画出他们的和,即以a和b为邻边的正方形过a和b共同起点的一条对角线以该对角线的终点为圆心再画一个半径为1的圆则c在此圆上,当c与该对角线同向时,|c|取最大值或最小值当c在原来单位圆的外面时,|c|取最大值:√2+1当c在原来单位圆的里面时,|c|取最小值:√2-1
 爱华网
爱华网