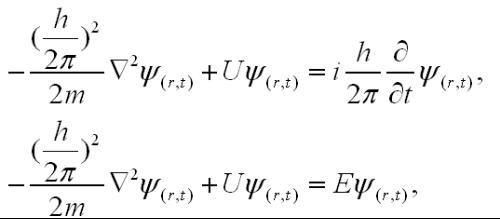薛定谔猫与第二定律确实矛盾
李耀诚
本文认为薛定谔猫问题中包含着真正的矛盾,因为猫的死是不可逆过程,热力学第二定律决定了猫的死活不可以并存!
1.薛定谔猫违反热力学第二定律
1935年厄文·薛定谔提出了一个理想实验:在封闭容器中有一只猫和一个由量子事件控制开关的毒气瓶。传统的量子力学认为:在未进行测量以前,毒气瓶开与关的可能性都存在,它们的态矢量相干叠加。于是,猫处于死和活的线性叠加态,只要没有人打开容器观察,猫就处于既可能已经死了又可能仍然活着的状态中。
大家都认为,这与常识相悖。但本文认为,这不仅仅与常识相悖,而且与热力学第二定律的精神相悖。猫的死是不可逆的,可以用很多种方法杀死猫,但任何方法都不能使猫复活。按照热力学第二定律,活猫态一旦转为死猫态,活猫态就不复存在。猫或者停留在活猫态,或者完全转入死猫态,活猫态与死猫态不可能同时存在!
虽然实验证实了量子力学的其他许多违反常识的论断,例如一个原子核可以同时出现在明显分开的两个区域等等,但是这些实验都不牵涉到热力学第二定律,都没有包含不可逆过程,所以不能用来说明薛定谔猫的矛盾。事实上,我们在各种量子力学实验中,从未观察到与不可逆过程纠缠着的量子叠加态。常识有可能错,但热力学第二定律不可能错,薛定谔猫问题的性质与EPR问题等佯谬不同,其中确实包含着矛盾。
有人可能会提出,“活猫态”与“死猫态”都是量子态,不能等同于现实中的“活猫”与“死猫”,所以不适用于热力学第二定律。这种观点显然是错误的。即便是量子态,“死猫态”的熵仍然远大于“活猫态”。按照统计物理学的观点,从“活猫量子态”到“死猫量子态”的转化肯定是不可逆的。不可逆过程一旦开始,就不受历史和环境的影响,自动完成,不可逆转。
按照波函数的统计诠释,一个由若干个子态叠加而成的叠加态中,各个子态需要等到被测量时才确定,被测出的概率等于它们的归一化的波函数的平方模。这是否可以被想象为,在测量前,各个量子态之间在不停地相互转换呢?我们应该可以根据热力学第二定律合理地假设:同一个量子叠加态的各个子态之间必须存在可逆转换。但是,“活猫态”与“死猫态”间的转换只能是不可逆的,“活猫态”与“死猫态”不可能存在于同一个量子叠加态!
为什么不是这样:当猫按照波函数规定的概率随机地进入死态时,按照热力学定律,不可以逆转回到活态,波函数就在此时坍缩?为什么非要等到有“意识”的人打开密闭容器的窥视孔瞥一眼,波函数才坍缩,猫的死活才能定下来呢?
2.“意识”的真正作用
传统的量子力学理论认为,要等到人进行“观察”时,波函数才会突然坍缩,从而确定猫的生死。但是,由人的“观察”引起的波函数坍缩,是在哪个瞬间发生的呢?是在待测量子态与测量仪器发生作用时呢,还是在人观看仪器的记录时呢?如果要依赖于人的观看,那么是在光线射入眼睛时呢,还是在视神经把讯号传送到大脑时呢,又还是在大脑得出分析结论时呢?毕竟有许多实验记录需要经过不止一人的长时间分析,才能得到结论。若干年后,另一些人重新分析,又可能会得出完全不同的结论。就薛定谔猫而言,人打开容器观察的第一眼,就很可能无法判断猫是昏迷还是死了,甚至可能只是睡着了。
如果波函数坍缩发生在待测量子态与测量仪器相互作用时,我们就可以把猫本身看作是一台测量仪器。在人“观察”以前,测量已经进行,坍缩已经发生,猫的死活已经被决定了。
双缝干涉实验中的判断路径实验也提供了一个例子,说明波函数的坍缩不需要依赖于人的“观察”。在双缝干涉实验中,粒子的德布罗意波穿过双缝,在干涉屏上形成干涉条纹。如果有人使用检测仪器判断粒子从哪条缝穿过,干涉条纹就消失,说明态矢量已经坍缩。但是,新的实验已经证实,粒子只要带上不同路径的标记,干涉条纹也消失。在这个过程中,人并没有检测粒子的标记。显然,粒子带上标记时,波函数就已经坍缩了,而此时人的“观察”尚未进行。
本文认为在量子测量过程中,人的“意识”的作用并不在于那透过观察孔的神奇的一瞥,而在于根据经验选择合适的仪器侵入待测量子系统。当然,在某些实验中眼睛本身就是合适的“观测仪器”,但在许多实验中,比如双缝实验,人如果只用眼睛看,并不能看见干涉图样。光束并不会因为有人“观察”,就自动在空中显现出干涉条纹来。人按照经验把照相底版放在光路上合适的地方,使波函数按预定的方式坍缩,才能“观察”到干涉图样。即使人在放置照相底版后离开了现场,波函数照样坍缩,干涉图样照样产生。所以,人的“意识”的真正作用就在于选择和放置测量仪器,而波函数的坍缩发生在待测量子态与所放置的仪器发生作用时,与人的“观察”并无直接关系。
但是,如果不是人的“意识”,那又是什么使波函数坍缩呢?
3.不可逆过程使波函数坍缩
从热力学第二定律的角度来看,薛定谔猫的死亡过程与量子测量过程并没有本质区别:活猫处于远离平衡态,这是靠它自身的生理活动维持的,由某个量子事件控制的一点点有毒化学物质可能会终止其生理活动,使之向平衡态转化。同样,威尔逊云雾室中的过饱和蒸汽也处于远离平衡态,高能粒子的扰动使之凝结为液滴,也就是向平衡态转化。在光电管、盖革计数器等探测器中,电场被用来收集游离电子,也都是不可逆过程,是待测粒子激发的游离电子使不可逆过程得以开始。照相底版上的AgI在光子作用下分解,也同样是不可逆过程。即使是人的眼睛,也是由光子在视神经上触发不可逆过程,从而看到影像的。
事实上,所有的量子测量过程都包含热力学不可逆过程。
一般来说,人如果要“观察”或者用仪器纪录量子事件,就需要从观察对象抽取少量信息,而根据热力学第二定律,在这种情况下必须同时发生不可逆过程才能保证总熵不减少。也就是说,热力学第二定律也确实规定,所有的量子测量都必然会引发不可逆过程。
假如量子叠加态引发的是可逆过程,量子叠加态与该可逆过程的初态、终态形成纠缠态。毫无疑问,按照量子态的叠加原理和波函数的统计诠释,它的各个子态以及与之纠缠的物理过程的初态或者终态的出现概率,应该等于其归一化的叠加系数的平方模。但是,当一个量子叠加态的部分子态引发不可逆过程时,由于按照统计物理学,不可逆过程的终态恢复到初态的概率可能非常小,于是就产生了矛盾:不可逆过程的初态与终态的出现概率,应该等于相关量子态的叠加系数的平方模呢,还是应该遵守统计物理学对不可逆过程的规定呢?这和薛定谔猫的矛盾是一样的,都反映了量子力学与热力学第二定律之间的矛盾。
既然所有量子测量过程都必然引发不可逆过程,那么它们也必然都有与薛定谔猫问题同样的矛盾。我们曾经把薛定谔猫看作是一台测量仪器,现在却发现,从热力学第二定律的角度来看,所有的量子测量仪器都是“薛定谔猫”!所以,薛定谔猫的矛盾是普遍存在的,是无法回避的。本文认为,正是这个矛盾导致波函数的坍缩。
可以设想:所有的量子测量,都必须由待测量子体系的某些子态触发不可逆过程,才能测出所需的信息。但同时,这个不可逆过程又迫使待测量子体系的波函数坍缩,因为只有波函数的坍缩,才能使热力学第二定律与波函数的统计诠释同时得到满足。所以,不是人的“观察”,而是不可逆过程使波函数坍缩。
除此之外,我们也应该看到,宇宙中经常发生的是非人为设置的不可逆过程。它们和薛定谔猫的死一样,与量子测量过程中的不可逆过程并没有本质区别;只要它们也与量子事件相纠缠,就必然也会产生薛定谔猫的矛盾,也会使波函数坍缩。(毕竟今天的宇宙看起来并不像是自大爆炸以来延续至今的量子叠加态。)不同的是,人能根据经验选择符合自己需要的不可逆过程来进行测量,这才是“意识”的真正作用。人为的量子测量仅仅是宇宙间经常发生的,能使相关量子体系的波函数坍缩的,大量不可逆过程中的个别例子。
4.不可逆过程—波函数坍缩
其实,在薛定谔猫问题中,首先发生的不可逆过程是毒气从瓶中向空间扩散。毒气本来封闭在毒气瓶内,某个量子事件打开瓶子,毒气也就扩散到整个容器中并毒死那只可怜的猫。
传统的量子力学理论认为:如果控制毒气瓶开关的量子事件的波函数为:
|ψ〉=α|↑〉+β|↓〉(1)
其中|↑〉态保持毒气瓶关闭,|↓〉态使毒气瓶打开,|α|2表示|↑〉态被测出的概率,|β|2表示|↓〉态被测出的概率,那么该量子事件与毒气瓶内毒气组成的复合体系波函数就是:
|Ψ〉=α|毒气不扩散〉|↑〉+β|毒气扩散〉|↓〉(2)
这样就使系统的线性叠加态得到保持,人“观察”时,发现毒气没有扩散的概率仍是|α|2;发现毒气已扩散,猫已被毒死的概率仍是|β|2。这符合量子力学波函数的统计诠释。
但是,(2)式与热力学第二定律显然不协调。按照第二定律,如果毒气有机会达至扩散态,即使毒气瓶再关闭,那些毒气,像《天方夜谭》里那个被渔夫救出来的瓶中妖魔那样被骗回瓶里去的概率,非常小。按照统计物理学,不可逆过程只有一个极小的概率P可以恢复初始状态。在扩散过程中,恢复到初态的概率
P=(v/V)N(3)
其中v为毒气瓶的容积,V为整个密闭容器的容积,N是毒气分子的数量。由于N~1022非常大,所以P非常接近0。
按照传统的量子力学波函数统计诠释,毒气扩散是在量子事件以|β|2的概率打开毒气瓶后,所以|毒气扩散〉态的概率就是|β|2,这个概率应保持不变,直到“测量”。而按照统计物理学及热力学第二定律,|扩散〉态与|不扩散〉态只要一有机会同时出现,就应立即向所有可到达态概率相等的平衡态转化,不受历史和环境的影响,原来的概率不会保持不变。究竟谁正确,是量子力学还是热力学第二定律?
其实,热力学第二定律与波函数的统计诠释都是经过大量实验证实了的,都不应该违背!
在第一节我们已经假设:在同一个量子叠加态的各子态间,必须存在可逆转换。所以,本文认为在复合体系中,只有大小为P的概率处于(2)式所描述的线性叠加态,因为这是系统能够恢复初态的概率,能够恢复初态就能够保持线性叠加态。而另外大小为(1-P)的概率则发生波函数坍缩,因为按照这个概率,系统不能由终态恢复到初态,系统或者停留在初态,或者完全进入终态。也就是说,按照大小为(1-P)|α|2的概率,毒气瓶实际保持关闭,毒气再也不会扩散;而按照大小为(1-P)|β|2的概率,毒气瓶实际打开,毒气扩散到整个密闭容器中,并把猫毒死。坍缩后,原来的量子叠加态就不复存在,未被选中的量子态完全消失,选中了的量子态组成新的叠加态,开始新的演化过程。只有这样,统计物理学规律与波函数的统计诠释才能够同时得到满足。
普遍来说,当某个量子事件引发一个物理过程时,应该以该物理过程能够恢复初态的概率P,作为量子体系保持线性叠加态的概率;而以该物理过程的不可逆概率(1-P),作为量子体系发生波函数坍缩的概率;当然,波函数坍缩时波函数的统计诠释仍然必须得到满足。这是一个“不可逆过程—波函数坍缩”联合事件,是既不违反热力学第二定律,又不破坏波函数的统计诠释的唯一可能的结果。显然,这个假说与所有已知的量子现象都不矛盾,而且是量子力学测量问题最简单、最合理的解释。
5.讨论
本文提出的“不可逆过程—波函数坍缩”假说与传统量子力学的主要不同点,就是引入了概率P,使波函数的坍缩不再依赖于人的“意识”,而且带有一定的随机性。
如果P等于1,物理过程就是可逆的,波函数不会坍缩,系统保持量子叠加态。这和传统的量子力学的描述完全一致,说明本文提出的“不可逆过程—波函数坍缩”假说与传统的量子力学是统一的。
如果P极小,比如在薛定谔猫的理想实验中,我们就不大可能观察到量子叠加态,波函数几乎肯定坍缩了,猫有非常接近|α|2的概率完全活着,有非常接近|β|2的概率完全死了。不可逆过程或者根本没有发生,而一旦发生了就不再回头。矛盾没有了,热力学第二定律与量子物理学得到了和谐的统一。这是在所有的量子测量中都会发生的情况,也是在所有与不可逆过程相联系的量子事件中都会发生的情况。当然猫确实也有可能处于死与活的线性叠加态,只是其概率P实在太小了。
“不可逆过程—波函数坍缩”假说与传统量子力学的区别主要表现在P比较大,但又不等于1时。这时,波函数坍缩的发生就有一个有可能被观察到的概率(1-P),它的某个子态在坍缩后仍存在的概率等于其归一化的叠加系数的平方模与(1-P)的乘积,其他子态完全消失,不可复原。同时,波函数还有一个保持叠加态,不发生坍缩的概率P。
 爱华网
爱华网