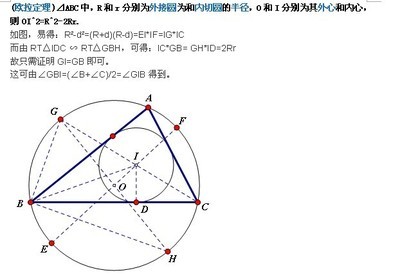
欧拉公式有4条(1)分式:a^r/(a-b)(a-c)+b^r/(b-c)(b-a)+c^r/(c-a)(c-b)当r=0,1时式子的值为0当r=2时值为1当r=3时值为a+b+c(2)复数由e^iθ=cosθ+isinθ,得到:sinθ=(e^iθ-e^-iθ)/2icosθ=(e^iθ+e^-iθ)/2(3)三角形设R为三角形外接圆半径,r为内切圆半径,d为外心到内心的距离,则:d^2=R^2-2Rr(4)多面体设v为顶点数,e为棱数,是面数,则v-e+f=2-2pp为欧拉示性数,例如p=0 的多面体叫第零类多面体p=1 的多面体叫第一类多面体等等其实欧拉公式是有4个的,上面说的都是多面体的公式
形式
- 对于任意实数,存在:
- 当时,欧拉公式的特殊形式为。(参见欧拉恒等式)
- 对于一个拥有个面、个顶角和条棱(边)的单联通多面体,必存在
- (参见欧拉示性数)
[编辑]证明
复分析领域:
- ,
- 将函数,和写成泰勒级数形式:
- 将代入可得:
定义函数
由于
可知不可能为0,因此以上定义成立。
则之导数为:
因此必须为一常数函数。
所以:
重新整理,即可得到:
[编辑]在复分析的应用
这公式可以说明当为实数时,函数可在复数平面描述一单位圆。且为此平面上一条连至原点的线与正实轴的交角(顺时钟的)。先前一个在复平面的复点只能用卡式坐标系描述,欧拉公式在此提供复点至极坐标的变换
任何复数皆可记为
在此
- 为实部
- 为虚部
- 为z的模
- ,其中
 爱华网
爱华网