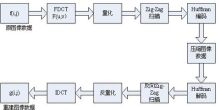
后又熟读程佩青的数字信号处理,对其中的前八章达到背诵的程度。
最后有熟读奥本海默的信号与系统与离散信号处理两本书,这两本书实在是厚啊,总共1000+页!
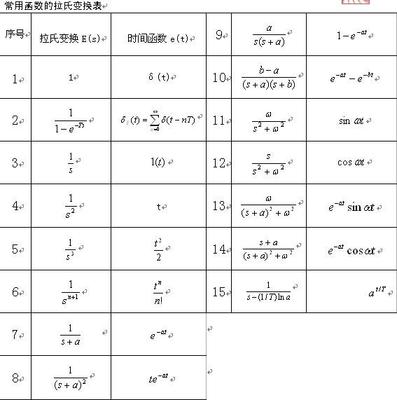
楼上很多人都说拉普拉斯变换没有实际的物理意义,相对于傅立叶变换明确的物理意义来说,拉普拉斯变换只是一个算子。
这种说法未免有失偏颇。
首先承认拉普拉斯变换确实起到算子的运用,然而其物理意义长期没有被人发现。
简单的说,大家都认可傅立叶变换的本质是一个信号可以表示成正弦信号的叠加,即无法进行傅立叶变换。
大家如果注意到傅立叶变换与拉普拉斯变换的关系可以发现,当s=jw时,傅拉普拉斯变换便等于傅立叶变换。可见傅立叶变换是拉普拉斯变换的特例。那么重点来了,如果一个是增长型的,比如e^2t,这个信号指数增长,是无法表示成等幅的正弦信号的叠加的。注意,傅立叶变换的物理意义是一个信号可以表示成等幅的正弦信号的叠加!!
这个等幅的概念有多少人忽略了!!!
那么,推广一下,不等幅的正弦信号(e^at*sint)便出现了!
数学波形是很容易想象的。
回到e^2t的问题,这个信号无法表示成等幅的正弦信号的叠加(傅立叶变换),那么它为何不能表示成增幅的正弦信号的叠加呢?
这就是拉普拉斯变换的物理意义!!!
上面这个信号在拉普拉斯变换中有一个收敛域,s>2.复频域如何表示自行想象。
其意义是啥呢?
因为收敛域包括s=4这条纵轴,这就意味着这个信号可以表示成∑e^4t*sinkwt这种增幅信号的叠加形式。
因为收敛域包括s=5这条纵轴,这就意味着这个信号可以表示成∑e^5t*sinkwt这种增幅信号的叠加形式。
s=6,7,8等等,道理如上。
那么可以发现,在拉普拉斯变换的收敛域内有无数条纵轴,在每一条纵轴上都可以写成一个不等幅正弦信号的叠加。
从这个角度来看,傅立叶变换只不过是s=0纵轴上,信号分解成等幅(特别强调这个等幅概念)正弦信号的叠加。
拉普拉斯变换确实有些明确的物理意义,只不过大多人没发现罢了。
 爱华网
爱华网