圆锥体积公式“V圆锥=V圆柱/3=πR2H/3”的数值计算论证 圆柱与圆锥

圆锥体积公式“V圆锥=V圆柱/3=πR²H/3”的数值计算论证

1

六年级小学生，先学习圆柱体积V圆柱=πR²H。再学习圆锥，且有“圆锥体积是等底等高圆柱体积的三分之一”的公式：V圆锥=V圆柱/3=πR²H/3。其中R是圆锥、圆柱底面的圆半径，H是圆锥、圆柱的高。

公式没有证明。教科书中提示：做两个模型，用倒水或倒沙子的方法，试一试它们有什么关系。連教科书的封面都是小朋友在做这个试验的图像。

2

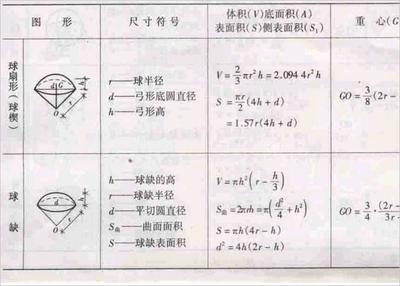
V圆锥=πR²H/3这个公式，要学到微积分时，才有证明，见图一。

取圆锥纵剖面的一半，是一个直角三角形。该直角三角形绕X轴旋转，便得圆锥体。以X表高H，0≦X≦H。以Y表半径R，0≦Y≦R。由Y/X=R/H得Y=RX/H。则其体积为V。

V=∫₀^Hπy²dX

=π∫₀^H(RX/H)²dX

=π∫₀^H(RX/H)²Dx

=πR²/H²∫₀^H（X²dX）

=πR²//H²(H³/3)

=πR²H/3，正是同高圆柱体积的三分之一

3

没有学过微积分的中小学生会发问：圆锥体积与圆柱体积1：3是怎样来的呢？我想，可以用数值计算的方法去诱导，去论证。他们会懂的。懂了，便能记住公式，也许还会引出一些趣味来。

可以设想，如果把圆锥变为一个同高的小圆柱，而体积不变，那么它的底面积一定要变小才行。变小到什么程度呢？设：这个小圆柱的底面半径为P，底面面积则为πp²，体积则为πp² H，由V圆锥=πR²H/3=πp²H可知，πp²= πR²/3。说明小圆柱底面积应是大圆柱底面积的1/3。见图二、图三。

那么，小圆柱底面积πp²怎样求呢？求出的值是否就是大圆柱底面积的1/3呢？请续看。

4

我们可对圆锥作许多橫截面，取这些橫截面面积的平均数，就是小圆柱的底面积了。取橫截面要平行、均匀、很密，这样平均数才精确、才能代表小圆柱的底面积。

一、现设原圆锥底面半径R=10，且将圆锥均匀平行切十刀，则每个橫截面的半径R_i由上而下为：

截面半径 R_i0123456789 10(11个橫截面)

R_i²0149162536496481 100

总和ΣR_i²= 385，

切十刀，用N=10表示，共有（n+1=11）个橫截面，注意，連同0是11个橫截面。

所以，平均橫截面积为ΣπR²/（n+1）=385π/11=35π，即小圆柱底面积为35π。而原大圆柱底面积为πR²=π*10*10=100π。两者一比，

35π/100π=0.35，与1/3=0.333333…不太符，有点误差，这是因为取的截面太少的原因。

二、重取原圆锥底面半径R=100，切100刀，各橫截面的半径R_i 由上而下为：

截面半径R_i01234 …9899100 (101个橫截面)

R_i²014916 …9604 980110000

总和ΣR_i²=338350，N=100刀，共n+1=101个橫截面。

平均橫截面积ΣπR²/（n+1）=338350π/101=3350π，即小圆柱底面积为3350π。而原大圆柱底面积为10000π，两者一比，

3350π/10000π=0.335，与1/3=0.333333…接近一些了。

三、再取原圆锥底面半径R=1000，切1000刀，各橫截面的半径R_i 由上而下为：

截面半径R_i01234…9989991000(1001个橫截面)

R_i²014916 …996004 9980011000000

总和333833500，N=1000刀，共1001个橫截面。

平均橫截面积ΣπR²/（n+1）=333833500π/1001=333500π，

即小圆柱底面积为333500π，而原大圆柱底面积为1000000π，两者一比，

333500π/1000000π=0.3335，与1/3=0.333333…更接近了。

综上所述，随着橫截面的增多，小圆柱底面积与原大圆柱底面积之比，由0.35→0.335→0.3335→0.33335→0.333335…橫截面→无穷多，其底面积之比将趋向于1/3。

5

有人问：这样笨算，若取R=10000000000，那要算到何时？不必着急，另有妙法呢。

其实，R_i² ： 01 4 9 1625 ……n²，是一组平方数数列，有它的求和公式：

ΣN ²=ΣR_i² =N (N+1) (2N+1) /6，当N=10时，ΣR_i²=10*11*21/6=385，当N=100时，ΣR_i²=100*101*201/6=338350。…

而R_i²的平均值=ΣR_i²/( N+1)= N (N+1) (2N+1)/6 / ( N+1)=N(2N+1)/6。计算更方便，不必一个个硬算。如，当N=10时，R_i²平均值=10*21/6=35。当N=100时，R_i²平均值=100*201/6=3350等等。实际上连ΣR_i²也不必计算，直接算R_i²的平均值就行(即小圆柱底面积)。

至于小圆柱底面积/原大圆柱底面积=πN(2N+1)/6 /πNN=2NN/6NN+1/6N=1/3+1/6N，当N→∞时，1/6N→0，所以：

小圆柱底面积/原大圆柱底面积=1/3。

这便是V圆锥= V圆柱 / 3=πR²H/3的来历。虽然是由数值计算来证实的，但这正是微积分的最基本的原理。全文完。

爱华网本文地址 » http://www.413yy.cn/a/25101013/183023.html