MATLAB中主要用int进行符号积分,用trapz,dblquad,quad,quad8等进行数值积分。 int(s)符号表达式s的不定积分 int(s,x) 符号表达式s关于变量x的不定积分 int(s,a,b) 符号表达式s的定积分,a,b分别为积分的上、下限 int(s,x,a,b) 符号表达式s关于变量x的定积分,a,b分别为积分的上、下限 trapz(x,y) 梯形积分法,x时表示积分区间的离散化向量,y是与x同维数的向量,表示被积函数,z返回积分值。 quad8(‘fun’,a,b,tol) 变步长数值积分,fun表示被积函数的M函数名,a,b分别为积分上、下限,tol为精度,缺省至为1e-3. fblquad(‘fun’,a,b,c,d)矩形区域二重数值积分,fun表示被积函数的M函数名,a,b分别为x的上、下限,c,d分别为y的上、下限. <?xml:namespace prefix="o" ns="urn:schemas-microsoft-com:office:office"?> 例1 计算二重积分 先编写四个M函数文件, %二重积分算法文件dblquad2.m functionS=dblquad2(f_name,a,b,c_lo,d_hi,m,n) %其中f_name为被积函数字符串,'c_lo'和'd_hi'是y的下限和上限函数,都是x的标量函数;a,b分别为x的下限和上限;m,n分别为x和y方向上的等分数(缺省值为100). ifnargin<7, n=100; end ifnargin<6, m=100; end ifm<2|n<2 error('Numner of intervals invalid'); end mpt=m+1; hx=(b-a)/m;x=a+(0:m)*hx; fori=1:mpt ylo=feval_r(c_lo,x(i)); yhi=feval_r(d_hi,x(i)); hy=(yhi-ylo)/n; for k=1:n+1 y(i,k)=ylo+(k-1)*hy; f(i,k)=feval_r(f_name,x(i),y(i,k));end G(i)=trapz(y(i,:),f(i,:)); end S=trapz(x,G); %被积函数eg3_fun.m function z=eg3_fun(x,y) z=1+x+y; %积分下限函数eg3_low.m function y=eg3_low(x) y=-sqrt(1-x^2); %积分上限函数eg3_up.m function y=eg3_up(x) y=sqrt(1-x^2); 保存后,在命令窗口用MATLAB代码: >>clear; >>dblquad2('eg3_fun',-1,1,'eg3_low','eg3_up') 结果为 ans=3.1383 为了得到更精确的数值解,需将区间更细化,比如x和y方向等分为1000分,MATLAB代码: >>clear;dblquad2('eg3_fun',-1,1,'eg3_low','eg3_up',1000,1000) 结果为 ans=3.1415。 此题也可用int符号计算求解,MATLAB代码为: >>clear; syms xy; >>iy=int(1+x+y,y,-sqrt(1-x^2),sqrt(1-x^2)); >>int(iy,x,-1,1) 结果为 ans=pi 例2 quad8计算定积分 %M函数fun1.m functiony=fun1(x) y=x.^4; 保存后,在命令窗口用MATLAB代码: >>clear; >>quad8('fun1',-2,2) >>vpa(quad8('fun1',-2,2),10)%以10位有效数字显示结果 结果为 ans=12.8000 ans=12.80000000 对于变步长数值积分,常用的有quad,quad8两种命令,quad使用自适应步长Simpson法,quad8使用自适应步长8阶Newton-Cotes法,我们建议用quad8,它不但精度较高,且对假收敛和假奇异积分具有一定的适应性,而quad较差.. 龙贝格积分法MATLAB程序代码 function[I,step]=Roberg(f,a,b,eps) whiletol>eps 自适应法求积分MATLAB程序代码 functionI=SmartSimpson(f,a,b,eps) functionq=SubSmartSimpson(f,a,b,eps) if(abs(QLeft+QRight-QA)<=eps) 线性振动响应分析的wilson θ积分法MATLAB代码 % see also http://www.matlabsky.com 常微分方程求解方法之四阶龙格-库塔算法matlab程序代码 function [x,y] =MyRunge_Kutta(fun,x0,xt,y0,PointNum,varargin) |
MATLAB与数值积分 matlab二重数值积分
更多阅读
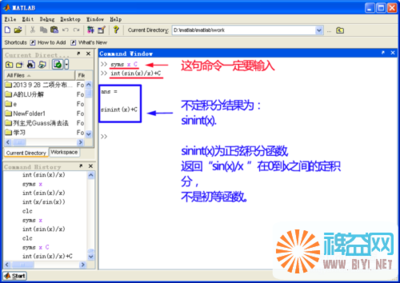
matlab求定积分与不定积分 matlab求定积分
matlab求定积分与不定积分——简介我们对一些函数进行定积分或者不定积分首先想到的都是求被积函数的原函数,但是一些被积函数的原函数无法用初等函数表示,或者即使能用初等函数表示,其表达式也是十分繁琐,很难求出来。下面我们借助mat
《无主之地2》操作化与数值化的矛盾 无主之地2存档修改器
(原载于《大众软件》)PC Xbox360 PS3个人评分4/5优点:壮阔的冒险,丰富的内容,在前作基础上做了许多改进丰富的装备,技能配合装备形成多种战术

常见翡翠赌石与场口组图 重生之翡翠赌石
常见翡翠赌石与场口[组图一] 发布时间: 2007-12-5 15:26:06 被阅览数: 36789 次 点击进入相关论坛随着经济的高速发展,中高档次翡翠的需求不断增多,缅甸矿山翡翠原料资源趋于枯竭,老厂翡翠原料越来越少;近几年市场发生了很大的变化,缅甸
剥皮魔 与兽同行系列二 与兽同行by易人北微盘
剥皮魔.与兽同行系列二楔子这是一栋邻近郊区,已经有些年月的平房。前后三间屋,带一个小院子,没有卫生间,上厕所要到街头的公共厕所在这一片老平房中,它是这么不起眼,看起来和其它房屋也没什么区别,除了它有一口井外井在院子里,可惜的是,井口被
MATLAB—求数值积分 matlab二重数值积分
由于有不少的微积分等式无解析解存在,所以必须以数值方法求解。MATLAB提供了一些函数用来求微积分的数值解。MATLAB提供最简单的积分函数是梯形法trapz,它的格式是trapz(x,y),其中x,y分别代表数目相同的数组或矩阵,而y与x的关系可以是
 爱华网
爱华网