本文选自3013年11月16日和23日的深圳市中小学教师继续教育课程《中学数学教师的教学研究与教研论文撰写指导》的学员考核作业
《圆周角与圆心角的关系》教学案例
龙珠中学 谢小梅
案例背景
1、我校教学改革情况
我校从2008年以来着力推行教育教学改革,实行以学生为本,以导学案、小组合作为支撑,以自学、互学、群学为基本学习模式,以个体自学、小组互学、展示提升、反馈测评为四个基本环节,以学生的参与度、学生的投入度、师生表达的精确性、师生对文本挖掘的深度、学习的结果五个角度对课堂进行评价的课堂教学模式。本课就是在我校课改大环境下的一节常规课。
2、教材和学生分析
本课是北师大版初中数学九年级下册第三章《圆》第三节《圆周角和圆心角的关系》第一课时。在学生学习了圆心角的概念以及有关性质的基础上,探究在同圆或等圆中,相等的弧所对的圆周角和圆心角的关系,在学生掌握了圆周角的定义和定理的基础上,起到了为下一节学习圆周角定理的两个推论及应用铺设了桥梁的作用。由于我校生源等实际情况的限制,从以往经验来看,学生学习积极性差,对本节知识掌握情况不够理想,部分学生对于圆周角的概念都难以弄明白,也存在一些学生找不到圆周角对应的圆心角的情况、对于圆周角与圆心角关系的探究与证明就更模糊了。
3、教学目标
知识目标:(1)根据圆周角定义判断一个角是不是圆周角
(2)理解并掌握圆周角与圆心角的关系
课堂组织目标:在学生自主学习的基础上,让所有学生都参与课堂,积极、放心、大胆的参与讨论,力争在圆周角的概念方面全体过关,在教学生圆周角与圆心角关系的知识上能够提高效果。
案例描述
(一)组内互学
学生在组内通过结对子等方式,相互交流知识点1:圆周角的概念。首先两人互相考察以下6种情况是不是圆的圆周角,并说明理由;在此基础上,由一方画出一个圆周角让对方画出对应的圆心角或者由一方画出圆心角由对方画出其中一个对应的圆周角。
组内互学一角:
甲:第一个是不是圆周角?为什么?
乙:不是,因为顶点不在圆上。第二个是不是圆周角?为什么?
甲:不是,因为有一边与圆除顶点外没有交点……
乙:……
……
甲:找到图(5)中圆周角所对的圆心角。
……
乙:动手画出来。让甲再找出与这个圆心角对应的另一个圆周角。
交流知识点2:圆周角与圆心角的关系,并准备在班级展示。
因为组员已经自学过导学案这部分内容,经过相互间交流,很快得出,在一个圆中,圆周角出现的三种情况。
学生经过阅读课本,大部分学生能够理解第一种情况下圆周角与圆心角的关系,理解∠B=∠AOC,也有小部分学生不明白,然后开始相互讲解,对于(2)(3)两种情况,部分学生能理解,但是讲解不够清楚,特别是第(3)情况,很多学生不能解决。
(二)全班展示
全班展示,圆周角与圆心角关系的(2)(3)两种情况。
丙:连接OB,延长与圆交于点D。(如下图)
师:这里有谁补充或订正吗?
生:没人回答。
师:这里要注意,延长线段时是要注意方向的,我们应说连接OB,并反向延长OB与圆交于点D或者改为连接BO,并延长BO与圆交于点D。
丙:然后(2)就转化成了(1)一样的问题。
丁:就是两个(1)的情况。(有点混乱,明白但没讲清楚)
戊:把右边挡住,左边就成了第(1)种情况,左边挡住右边就成了第(1)种情况。
师:你上来演示给大家看。
戊上黑板,用手将(下(2)图)右半部分挡住,老师给他一本书,他用书挡住,这是下面发出恍然大悟的声响,哦……
接下来,学生通过(1)得出,∠ABO=∠AOD,∠CBO=∠COD,然后等式左右两边相加,得出结论:∠CBA=∠COA,老师再给出2分钟时间相互在进行一次小沟通。
师:接下来,我们继续来研究第(3)种情况。
己:连接BO,并延长BO与圆交于点D(如下图(3))。
师:很好,这次非常正确。
己:然后∠ABD=∠AOD,∠CBD=∠COD,两边一减,∠CBA=∠COA(很简洁,但大部分人都没听懂。)
己急了,开始再次讲解,然而有一部分人仍然发懵,到最后已经忘记了这个题到底要干什么。
师:好了,大家静一静,我们先清醒一下,这个题到底要干什么?要得出什么结论?(在老师的提醒下,有学生很清楚的回答了这个问题,要找寻∠ABC与∠AOC的关系,并且我们猜测∠ABC=∠AOC)。
师:为了帮助己同学讲清楚这个问题,老师现在用几何画板给大家演示。(面向己,你来说,我来做。)
接下来,老师应用几何画板,通过隐藏其余部分,以及运用几个图之间的对比帮助己同学顺利的完成了题目的讲解。
师:接下来,给3分钟的时间,大家再相互讲一讲。
通过对三种情况的分类讨论,我们得到结论:_____________________.老师再对分类讨论以及前面用到的划归思想做一个小总结。
(三)分组展示
组内学生被分为A、B两组,B组学生上白板轮换讲解“展示提升”部分1-3三个题目,要求人人上场,弱一点的讲简单的1题,强一些的讲靠后的题目。A组学生自主完成1-4题,有需要时帮助B组学生讲解1-3题。
展示提升题目如下:
1.填空:
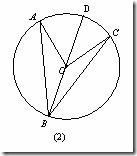
2.如图,OA、OB、OC都是⊙O的半径,∠AOB=2∠BOC,∠ACB与∠BAC的大小有什么关系?为什么?
3.如图,在⊙O中,OA、OB是半径,且AB=5cm,已知∠ACB=30°,求⊙O的半径。
4.如图,OC垂直于⊙O的弦AB于C,交⊙O于点D,已知∠ADB=60°,OC=2,求⊙O的半径和AB的长。
案例反思:
1、尽量让每一个人都参与课堂
本来知识点1圆周角的概念是比较简单的内容,课前我认为学生会一带而过,没想到学生的表现非常的积极、热情,那些班级成绩最糟糕的学生都参与到其中,虽然这样可能会多花一些时间,但是相对于看到每一个学生都参与课堂学习的收获来说,我认为这点时间的花费是值得的,而这也说明学生不参与课堂不是他本身不愿意,而是他真的遇到了困难,所以创造能让他们参与的环境能更好的激发他们的热情。
2、主动获取的知识更牢固
数学课要注重引导学生探索与获取知识的过程而不单注重学生对知识内容的认识,因为“过程”不仅能引导学生更好地理解知识,还能够引导学生在活动中思考,更好地感受知识的价值,增强应用数学知识解决问题的意识。本课中,学生跟随老师的引导利用课本和导学案自主学习。老师进行指导,每一个结论都需要学生根据课本或导学案的指引,自主总结,归纳。在探索圆心角与圆周角的关系的第二种情况的时候,当丙、丁的讲解遇到困难的时候,老师没有马上去“救火”,而是继续等待学生思考,最后在同学们的努力下由戊给大家做了堪称“完美”的讲解。在第(3)种情况的讲解过程中,老师帮助同学利用几何画板完成了讲解,这些由学生自主获取的知识更牢固,而且让学生养成乐于钻研、不轻易放弃的品质。
3、不走形式,注重实质
课改要求转变教师的角色为学生学习的组织者、引导者、合作者与共同研究者。这体现在一方面教师不再是不停的告诉学生这个结论,那个结论,而是引导学生通过自身思考,交流与探究得到解决问题的思路与方法,教师成为了学生的伙伴、甚至学生,在课堂上除了导引学生活动,还要认真聆听学生的“教”。另一方面,当学生的语言不规范或者知识点出了问题,或者讲解遇到了困难的时候,老师通过适当的帮助,让讲解的学生讲解清楚,聆听的学生理解清楚。在学生作辅助线语言出问题时马上指出来,而在学生讲解第(2)(3)种情况遇到困难时,作为合作者出现和学生一起解决问题。
4、留适当的时间给学生整理知识
每当一个知识点讲解完毕时,给出2-3分钟的时间,让明白了的学生对知识进行梳理,让还稍有迷糊的学生能够及时向同学请教,这对学生对知识的掌握是有好处的,从后面的反馈情况来看,这节课下来学生对圆周角的概念基本全员掌握,圆周角与圆心角的关系的结论及证明学生的掌握情况也不错。
 爱华网
爱华网