MATLAB插值与拟合

§1曲线拟合

实例：温度曲线问题

气象部门观测到一天某些时刻的温度变化数据为：

试描绘出温度变化曲线。

曲线拟合就是计算出两组数据之间的一种函数关系，由此可描绘其变化曲线及估计非采集数据对应的变量信息。

曲线拟合有多种方式，下面是一元函数采用最小二乘法对给定数据进行多项式曲线拟合，最后给出拟合的多项式系数。

1.线性拟合函数：regress()

调用格式： b=regress(y,X)

[b,bint,r,rint,stats]= regress(y,X)

[b,bint,r,rint,stats]= regress(y,X,alpha)

说明：b=regress(y,X)返回X处y的最小二乘拟合值。该函数求解线性模型：

y=Xβ+ε

β是p´1的参数向量；ε是服从标准正态分布的随机干扰的n´1的向量；y为n´1的向量；X为n´p矩阵。

bint返回β的95%的置信区间。r中为形状残差，rint中返回每一个残差的95%置信区间。Stats向量包含R²统计量、回归的F值和p值。

例1：设y的值为给定的x的线性函数加服从标准正态分布的随机干扰值得到。即y=10+x+ε；求线性拟合方程系数。

程序： x=[ones(10,1) (1:10)’]

y=x*[10;1]+normrnd(0,0.1,10,1)

[b,bint]=regress(y,x,0.05)

结果： x =

11

12

13

14

15

16

17

18

19

1 10

y =

10.9567

11.8334

13.0125

14.0288

14.8854

16.1191

17.1189

17.9962

19.0327

20.0175

b =

9.9213

1.0143

bint =

9.7889 10.0537

0.99301.0357

即回归方程为：y=9.9213+1.0143x

2.多项式曲线拟合函数：polyfit( )

调用格式： p=polyfit(x,y,n)

[p,s]= polyfit(x,y,n)

说明：x,y为数据点，n为多项式阶数，返回p为幂次从高到低的多项式系数向量p。矩阵s用于生成预测值的误差估计。(见下一函数polyval)

例2：由离散数据

拟合出多项式。

程序：

x=0:.1:1;

y=[.3 .5 1 1.4 1.6 1.9 .6 .4 .8 1.5 2]

n=3;

p=polyfit(x,y,n)

xi=linspace(0,1,100);

z=polyval(p,xi); %多项式求值

plot(x,y,’o’,xi,z,’k:’,x,y,’b’)

legend(‘原始数据’,’3阶曲线’)

结果：

p =

16.7832-25.745910.9802 -0.0035

多项式为：16.7832x³-25.7459x²+10.9802x-0.0035

曲线拟合图形：

也可由函数给出数据。

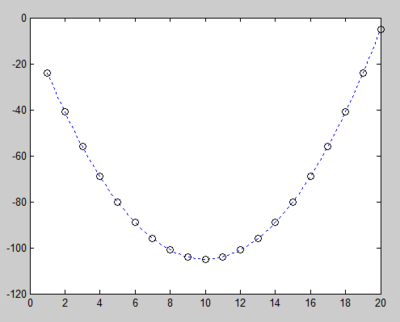
例3：x=1:20,y=x+3*sin(x)

程序：

x=1:20;

y=x+3*sin(x);

p=polyfit(x,y,6)

xi=1inspace(1,20,100);

z=poyval(p,xi);%多项式求值函数

plot(x,y,’o’,xi,z,’k:’,x,y,’b’)

legend(‘原始数据’,’6阶曲线’)

结果：

p =

0.0000-0.00210.0505-0.59713.6472-9.729511.3304

再用10阶多项式拟合

程序：x=1:20;

y=x+3*sin(x);

p=polyfit(x,y,10)

xi=linspace(1,20,100);

z=polyval(p,xi);

plot(x,y,'o',xi,z,'k:',x,y,'b')

legend('原始数据','10阶多项式')

结果：p =

Columns 1 through 7

0.0000-0.00000.0004-0.01140.1814-1.8065 11.2360

Columns 8 through 11

-42.086188.5907-92.8155 40.2671

可用不同阶的多项式来拟合数据，但也不是阶数越高拟合的越好。

3.多项式曲线求值函数：polyval( )

调用格式： y=polyval(p,x)

[y,DELTA]=polyval(p,x,s)

说明：y=polyval(p,x)为返回对应自变量x在给定系数P的多项式的值。

[y,DELTA]=polyval(p,x,s) 使用polyfit函数的选项输出s得出误差估计YDELTA。它假设polyfit函数数据输入的误差是独立正态的，并且方差为常数。则Y DELTA将至少包含50%的预测值。

4.多项式曲线拟合的评价和置信区间函数：polyconf( )

调用格式： [Y,DELTA]=polyconf(p,x,s)

[Y,DELTA]=polyconf(p,x,s,alpha)

说明：[Y,DELTA]=polyconf(p,x,s)使用polyfit函数的选项输出s给出Y的95%置信区间YDELTA。它假设polyfit函数数据输入的误差是独立正态的，并且方差为常数。1-alpha为置信度。

例4：给出上面例1的预测值及置信度为90%的置信区间。

程序：x=0:.1:1;

y=[.3 .5 1 1.4 1.6 1.9 .6 .4 .8 1.5 2]

n=3;

[p,s]=polyfit(x,y,n)

alpha=0.05;

[Y,DELTA]=polyconf(p,x,s,alpha)

结果： p =

16.7832-25.745910.9802 -0.0035

s =

R: [4x4double]

df: 7

normr: 1.1406

Y =

Columns 1 through 7

-0.00350.85381.29701.42661.34341.14800.9413

Columns 8 through 11

0.82380.89631.25942.0140

DELTA =

Columns 1 through 7

1.36391.15631.15631.15891.13521.12021.1352

Columns 8 through 11

1.15891.15631.15631.3639

5.稳健回归函数：robust( )

稳健回归是指此回归方法相对于其他回归方法而言，受异常值的影响较小。

调用格式： b=robustfit(x,y)

[b,stats]=robustfit(x,y)

[b,stats]=robustfit(x,y,’wfun’,tune,’const’)

说明：b返回系数估计向量；stats返回各种参数估计；’wfun’指定一个加权函数；tune为调协常数；’const’的值为’on’(默认值)时添加一个常数项；为’off’时忽略常数项。

例5：演示一个异常数据点如何影响最小二乘拟合值与稳健拟合。首先利用函数y=10-2x加上一些随机干扰的项生成数据集，然后改变一个y的值形成异常值。调用不同的拟合函数，通过图形观查影响程度。

程序：x=(1:10)’;

y=10-2*x+randn(10,1);

y(10)=0;

bls=regress(y,[ones(10,1) x]) %线性拟合

brob=robustfit(x,y) %稳健拟合

scatter(x,y)

hold on

plot(x,bls(1)+bls(2)*x,’:’)

plot(x,brob(1)+brob(2)*x,’r‘)

结果 ： bls =

8.4452

-1.4784

brob =

10.2934

-2.0006

分析：稳健拟合(实线)对数据的拟合程度好些，忽略了异常值。最小二乘拟合(点线)则受到异常值的影响，向异常值偏移。

6.向自定义函数拟合

对于给定的数据，根据经验拟合为带有待定常数的自定义函数。

所用函数：nlinfit( )

调用格式：[beta,r,J]=nlinfit(X,y,’fun’,betao)

说明：beta返回函数’fun’中的待定常数；r表示残差；J表示雅可比矩阵。X,y为数据；‘fun’自定义函数；beta0待定常数初值。

例6：在化工生产中获得的氯气的级分y随生产时间x下降，假定在x≥8时，y与x之间有如下形式的非线性模型：

现收集了44组数据，利用该数据通过拟合确定非线性模型中的待定常数。

xyxyxy

80.49160.43280.41

80.49180.46280.40

100.48180.45300.40

100.47200.42300.40

100.48200.42300.38

100.47200.43320.41

120.46200.41320.40

120.46220.41340.40

120.45220.40360.41

120.43240.42360.36

140.45240.40380.40

140.43240.40380.40

140.43260.41400.36

160.44260.40420.39

160.43260.41

首先定义非线性函数的m文件：fff6.m

function yy=model(beta0,x)

a=beta0(1);

b=beta0(2);

yy=a+(0.49-a)*exp(-b*(x-8));

程序：

x=[8.00 8.00 10.00 10.00 10.00 10.00 12.00 12.00 12.00 14.0014.00 14.00...

16.00 16.00 16.00 18.00 18.00 20.00 20.00 20.00 20.00 22.00 22.0024.00...

24.00 24.00 26.00 26.00 26.00 28.00 28.00 30.00 30.00 30.00 32.0032.00...

34.00 36.00 36.00 38.00 38.00 40.00 42.00]';

y=[0.49 0.49 0.48 0.470.48 0.47 0.46 0.46 0.45 0.43 0.45 0.43 0.43 0.44 0.43...

0.43 0.46 0.42 0.42 0.43 0.41 0.41 0.40 0.42 0.40 0.40 0.41 0.400.41 0.41...

0.40 0.40 0.40 0.38 0.41 0.40 0.40 0.41 0.38 0.40 0.40 0.390.39]';

beta0=[0.30 0.02];

betafit = nlinfit(x,y,'sta67_1m',beta0)

结果：betafit =

0.3896

0.1011

即：a=0.3896 ，b=0.1011 拟合函数为：

§2 插值问题

在应用领域中，由有限个已知数据点，构造一个解析表达式，由此计算数据点之间的函数值，称之为插值。

实例：海底探测问题

某公司用声纳对海底进行测试，在5×5海里的坐标点上测得海底深度的值，希望通过这些有限的数据了解更多处的海底情况。并绘出较细致的海底曲面图。

一、一元插值

一元插值是对一元数据点(x_i,y_i)进行插值。

1．线性插值：由已知数据点连成一条折线，认为相临两个数据点之间的函数值就在这两点之间的连线上。一般来说，数据点数越多，线性插值就越精确。

调用格式：yi=interp1(x,y,xi,’linear’)%线性插值

zi=interp1(x,y,xi,’spline’) %三次样条插值

wi=interp1(x,y,xi,’cubic’) %三次多项式插值

说明：yi、zi、wi为对应xi的不同类型的插值。x、y为已知数据点。

例1：已知数据：

求当x_i=0.25时的y_i的值。

程序：

x=0:.1:1;

y=[.3 .5 1 1.4 1.6 1 .6 .4 .8 1.5 2];

yi0=interp1(x,y,0.025,'linear')

xi=0:.02:1;

yi=interp1(x,y,xi,'linear');

zi=interp1(x,y,xi,'spline');

wi=interp1(x,y,xi,'cubic');

plot(x,y,'o',xi,yi,'r+',xi,zi,'g*',xi,wi,'k.-')

legend('原始点','线性点','三次样条','三次多项式')

结果：yi0 = 0.3500

要得到给定的几个点的对应函数值，可用：

xi =[ 0.2500 0.35000.4500]

yi=interp1(x,y,xi,'spline')

结果：

yi =1.20881.5802 1.3454

(二) 二元插值

二元插值与一元插值的基本思想一致，对原始数据点(x,y,z)构造见世面函数求出插值点数据(xi,yi,zi)。

一、单调节点插值函数，即x,y向量是单调的。

调用格式1：zi=interp2(x,y,z,xi,yi,’linear’)

‘liner’ 是双线性插值 (缺省)

调用格式2：zi=interp2(x,y,z,xi,yi,’nearest’)

’nearest’ 是最近邻域插值

调用格式3：zi=interp2(x,y,z,xi,yi,’spline’)

‘spline’是三次样条插值

说明：这里x和y是两个独立的向量，它们必须是单调的。z是矩阵，是由x和y确定的点上的值。z和x,y之间的关系是z(i,:)=f(x,y(i))z(:,j)=f(x(j),y)即：当x变化时，z的第i行与y的第i个元素相关，当y变化时z的第j列与x的第j个元素相关。如果没有对x,y赋值，则默认x=1:n,y=1:m。n和m分别是矩阵z的行数和列数。

例2：已知某处山区地形选点测量坐标数据为：

x=0 0.51 1.5 22.5 3 3.54 4.5 5

y=0 0.51 1.5 22.5 3 3.54 4.5 55.5 6

海拔高度数据为：

z=89 90 87 85 92 91 96 93 90 87 82

92 96 98 99 9591 89 86 84 82 84

96 98 95 92 9088 85 84 83 81 85

80 81 82 89 9596 93 92 89 86 86

82 85 87 98 9996 97 88 85 82 83

82 85 89 94 9593 92 91 86 84 88

88 92 93 94 9589 87 86 83 81 92

92 96 97 98 9693 95 84 82 81 84

85 85 81 82 8080 81 85 90 93 95

84 86 81 98 9998 97 96 95 84 87

80 81 85 82 8384 87 90 95 86 88

80 82 81 84 8586 83 82 81 80 82

87 88 89 98 9997 96 98 94 92 87

其地貌图为：

对数据插值加密形成地貌图。

程序：

x=0:.5:5;

y=0:.5:6;

z=[89 90 87 85 92 91 96 93 90 87 82

92 96 98 9995 91 89 86 84 82 84

96 98 95 9290 88 85 84 83 81 85

80 81 82 8995 96 93 92 89 86 86

82 85 87 9899 96 97 88 85 82 83

82 85 89 9495 93 92 91 86 84 88

88 92 93 9495 89 87 86 83 81 92

92 96 97 9896 93 95 84 82 81 84

85 85 81 8280 80 81 85 90 93 95

84 86 81 9899 98 97 96 95 84 87

80 81 85 8283 84 87 90 95 86 88

80 82 81 8485 86 83 82 81 80 82

87 88 89 9899 97 96 98 94 92 87];

mesh(x,y,z) %绘原始数据图

xi=linspace(0,5,50);%加密横坐标数据到50个

yi=linspace(0,6,80);%加密纵坐标数据到60个

[xii,yii]=meshgrid(xi,yi);%生成网格数据

zii=interp2(x,y,z,xii,yii,'cubic');%插值

mesh(xii,yii,zii)%加密后的地貌图

holdon% 保持图形

[xx,yy]=meshgrid(x,y);%生成网格数据

plot3(xx,yy,z+0.1,’ob’)%原始数据用‘O’绘出

2、二元非等距插值

调用格式：zi=griddata(x,y,z,xi,yi,’指定插值方法’)

插值方法有：linear% 线性插值 (默认)

bilinear% 双线性插值

cubic% 三次插值

bicubic% 双三次插值

nearest% 最近邻域插值

例：用随机数据生成地貌图再进行插值

程序：

x=rand(100,1)*4-2;

y=rand(100,1)*4-2;

z=x.*exp(-x.^2-y.^2);

ti=-2:.25:2;

[xi,yi]=meshgrid(ti,ti); % 加密数据

zi=griddata(x,y,z,xi,yi);% 线性插值

mesh(xi,yi,zi)

hold on

plot3(x,y,z,'o')

该例中使用的数据是随机形成的，故函数griddata可以处理无规则的数据。

爱华网本文地址 » http://www.413yy.cn/a/25101013/176851.html