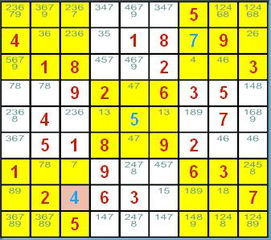
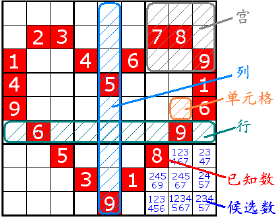
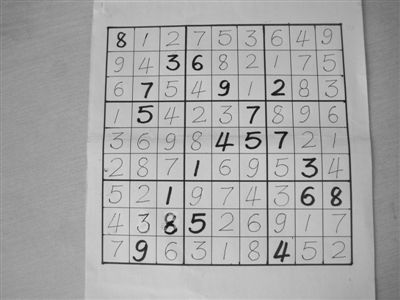
Noip2009靶形数独解题报告(位运算版)
语言:C++作者:副博主
实现方法:搜索
技巧:位运算
此题以及类似题目(如八皇后),最明智的选择都是位运算实现。
理由:
思考:普通搜索时间都浪费到哪里了?
答曰:1.查哪一位是空的,也就是没填;
2.试探这一个空位可否填这个数或者找出这位可填的数。于是你要把这一行的数过一遍,再把这一列的数过一遍,再把所在的小九宫格过一遍。
每次都这么做,时间就浪费了。
思考:能否用一步运算做到1.找空位;2.找出可填的数。
答曰:可以。位运算技巧多多,是这类搜索题的最佳选择。
如果你对位运算不是很了解,可以先看matrix67大牛对位运算的讲解(4节内容),以下是他的博客地址:
http://www.matrix67.com/blog/archives/263
你若是理解了其八皇后的做法,那么你的位运算已经差不多了,足以用位运算解此题。
以下是我的源程序+简略的解释:
(看的顺序当然是先看主程。)由于新浪博客字数限制,故删除了一些东西(如评测结果),甚至不得不删掉注释里的空格,导致注释和代码挤的很难看。
#include<stdio.h>
#include<math.h>
inth[10]={},hs[10]={},zs[10]={},xj[5][5]={},hq[10]={};//全都清零一下,具体意思下面解释。
intans=-1,st[10],a[10][10];
void make()//这个是算分值,更新ans
{
int sum=0,i,j;
for (i=1;i<5;i++)
{for (j=i;j<11-i;j++)
sum+=(a[i][j]+a[10-i][j])*(5+i);
for (j=i+1;j<10-i;j++)
sum+=(a[j][i]+a[j][10-i])*(5+i);
}
sum+=a[5][5]*10;
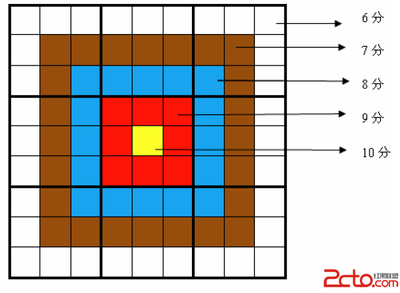
if (sum>ans) ans=sum;
}
void dfs(int k)//搜索部分,k不表示搜索第k行,而是第st[k]行
{
if (k==10) make();//k=10表示九行都搞定了,开始算分
else
{
intx,y,j,pos,p,i=st[k];//i表示第i行,j表示第j列
x=511-h[i];//511(10)=111,111,111(2),故此行的意思是将第i行缺位取出来
此时x中1表示缺位,y与x同
y=x&-x;//y是取出本行第一个缺位,在这一次搜索里就搜索这个缺位
h[i]|=y;//下一次搜索时,这一位已填,故把缺位补上
j=(int)log2(y)+1;//j就是y用二进制表示1所在的位数,即j列
pos=511-(hs[i]|zs[j]|xj[(i-1)/3][(j-1)/3]);//这一步是取出可以填哪些数
while (pos>0)
{p=pos&-pos;//取出可以填的一个数
pos-=p;//去掉已填的数
a[i][j]=(int)log2(p)+1;//填入a中
hs[i]|=p;//修改hs,zs,xj,这个数已用过,‘或’写成‘+’也行
zs[j]|=p;
xj[(i-1)/3][(j-1)/3]|=p;
if (x==y) dfs(k+1);//若x=y,则这一行只有一个空,即现在已填的空,故搜索k+1
else dfs(k);//若x<>y,则这一行还有空没填,继续搜索这一行
hs[i]-=p;//搜索完,还原hs,zs,xj
zs[j]-=p;
xj[(i-1)/3][(j-1)/3]-=p;
};
h[i]-=y;//s搜索完,还原h[i]
};
}
int main()
{
int i,j,p0;
for (i=1;i<10;i++)
for (j=1;j<10;j++)
{scanf("%d",&a[i][j]);//读入数独,数组a记的是数独。
if (a[i][j]>0)
{h[i]|=1<<(j-1);//数组h记的是某一行填数情况
//h[i]写成二进制,第j位为0,表示a[i][j]=0,即没填同理第j位为1,表示a[i][j]>0,已填数
p0=1<<(a[i][j]-1);//p0写成二进制,第k位为1,表示数字k已用过
if(((hs[i]&p0)!=0)||((zs[j]&p0)!=0)||
((xj[(i-1)/3][(j-1)/3]&p0)!=0))
{printf("-1n");return0;};//这个判断是看数独有没有错,即某一行(列,九宫格)是否有同一数字出现两次
hs[i]|=p0;//数组hs记的是某一行数字用的情况
//hs[i]写成二进制,第j位为0,表示i行,j没用过
同理第j位为1,表示i行,j用过
zs[j]|=p0;//数组zs记的是某一列(纵行)数字用的情况,意义同hs
xj[(i-1)/3][(j-1)/3]|=p0;//数组xj记的是某一小九宫格数字用的情况,意义同hs
}//九个小九宫格分别是xj[0][0] xj[0][1] xj[0][2]
xj[1][0] xj[1][1] xj[1][2]
xj[2][0] xj[2][1] xj[2][2]
else hq[i]++;}//数组hq记的是某一行缺数的个数,唯一的优化的组成部分。
for (i=1;i<10;i++) st[i]=i;//数组st记的是搜索各行的顺序,就是先搜哪一行,再搜哪一行
for (i=1;i<9;i++)//此部分是按各行空缺数的个数将st从小到大排序
for (j=i+1;j<10;j++)//使得一会搜的时候,先搜缺数少的行,这也就是唯一的优化
if (hq[st[i]]>hq[st[j]])
{st[i]^=st[j];//交换两数位运算版
st[j]^=st[i];
st[i]^=st[j];}
for (i=1;hq[st[i]]==0;i++);//考虑到某一行缺数可能为0,故先找到缺数的行
dfs(i);//开始搜索
printf("%dn",ans);//ans就是答案
return 0;
}
怎么样,搜索的很朴素吧,但同样很快,能AC这道题。
 爱华网
爱华网