绝对值的三角不等式;不等式证明的基本方法 绝对值三角不等式练习
1、掌握绝对值的三角不等式;
2、掌握不等式证明的基本方法
三. 知识分析
[绝对值的三角不等式]
定理1 若a,b为实数,则 ,当且仅当ab≥0时,等号成立。
几何说明:(1)当ab>0时,它们落在原点的同一边,此时a与-b的距离等于它们到原点距离之和。
(2)如果ab<0,则a,b分别落在原点两边,a与-b的距离严格小于a与b到原点距离之和(下图为ab<0,a>0,b<0的情况,ab<0的其他情况可作类似解释)。
|a-b|表示a-b与原点的距离,也表示a到b之间的距离。
定理2 设a,b,c为实数,则 ,等号成立 ,即b落在a,c之间。
推论1
推论2
[不等式证明的基本方法]
1、比较法是证明不等式的一种最基本的方法,也是一种常用的方法,基本不等式就是用比较法证得的。
比较法有差值、比值两种形式,但比值法必须考虑正负。
比较法证不等式有作差(商)、变形、判断三个步骤,变形的主要方向是因式分解、配方,判断过程必须详细叙述。
如果作差后的式子可以整理为关于某一个变量的二次式,则可考虑用到判别式法证。
2、所谓综合法,就是从题设条件和已经证明过的基本不等式出发,不断用必要条件替换前面的不等式,直至推出要证明的结论,可简称为“由因导果”,在使用综合法证明不等式时,要注意基本不等式的应用。
所谓分析法,就是从所要证明的不等式出发,不断地用充分条件替换前面的不等式,或者是显然成立的不等式,可简称“执果索因”,在使用分析法证明不等式时,习惯上用“ ”表述。
综合法和分析法是两种思路截然相反的证明方法,其中分析法既可以寻找解题思路,如果表述清楚,也是一个完整的证明过程.注意综合法与分析法的联合运用。
3、反证法:从否定结论出发,经过逻辑推理,导出矛盾,证实结论的否定是错误的,从而肯定原结论是正确的证明方法。
4、放缩法:欲证A≥B,可通过适当放大或缩小,借助一个或多个中间量,使得 , ,再利用传递性,达到证明的目的.这种方法叫做放缩法。
【典型例题】
例1、已知函数 ,设a、b∈R,且a≠b,求证:
思路:本题证法较多,下面用分析法和放缩法给出两个证明:
证明:
证法一:
①
当ab≤-1时,式①显然成立;
当ab>-1时,式① ②
∵a≠b,∴式②成立。故原不等式成立。
证法二:当a=-b时,原不等式显然成立;
当a≠-b时,
∴原不等式成立。
点评:此题还可以用三角代换法,复数代换法、数形结合等证明,留给读者去思考。
例2、设m等于|a|、|b|和1中最大的一个,当|x|>m时,求证: 。
思路:本题的关键是对题设条件的理解和运用,|a|、|b|和1这三个数中哪一个最大?如果两两比较大小,将十分复杂,但我们可以得到一个重要的信息:m≥|a|、m≥|b|、m≥1。
证明:
故原不等式成立。
点评:将题设条件中的文字语言“m等于|a|、|b|、1中最大的一个”转化为符号的语言“m≥|a|、m≥|b|、m≥1”是证明本题的关键。
例3、函数 的定义域为[0,1]且 。当 ∈[0,1], 时都有 ,求证: 。
证明:不妨设 ,以下分两种情形讨论。
若
则
,若
则
综上所述
点评:对于绝对值符号内的式子,采用加减某个式子后,重新组合,运用绝对值不等式的性质变形,是证明绝对值不等式的典型方法。
例4、已知a>0,b>0,求证: 。
思路:如果用差值比较法,下一步将是变形,显然需要通分,是统一通分,还是局部通分?从题目结构特点看,应采取局部通分的方法。
证明:
①
②
∴原不等式成立。
点评:在上面得到①式后,其分子的符号可由题设条件作出判断,但它没有②明显,所以,变形越彻底,越有利于最后的判断,本题还可以用比值比较法证明,留给读者去完成。
例5、设x>0,y>0,且x≠y,求证:
思路:注意到x、y的对称性,可能会想到重要不等式,但后续思路不好展开,故我们可采用分析法,从消去分数指数幂入手。
证明:∵x>0,y>0,且x≠y,
点评:在不便运用比较法或综合法时,应考虑用分析法。应注意分析法表述方法,其中寻求充分条件的语句常用符号“ ”表述。本题应用了分析法,既找到了解题思路,又使问题完满地得到了解决,可谓一举两得。
例6、已知a、b、c∈R+,求证: 。
思路:因不等式的左边的两个因式都可以进行因式分解。结合a、b、c∈R+的条件,运用重要不等式,采用综合法进行证明。
解析:
即
点评:用重要不等式证明不等式,一要注意重要不等式适用的条件,二要为运用重要不等式创造条件。另外,同向不等式相加或相乘,在综合法中常用到。
例7、证明:对于任意实数x、y,有
思路:采取分析法和比较法二者并用的方法来处理。
证明:用分析法
不等式②显然成立,下面证明不等式①
同号
,即
点评:上述证明中,前半部分用的是分析法,后半部分用的是比较法,两种方法结合使用,使问题较容易解决,这一点应加以注意。
例8、(1)用反证法证明以下不等式:已知 ,求证p+q≤2。
(2)试证: (n≥2)。
思路:运用放缩法进行证明。
证明:(1)设p+q>2,则p>2-q,
这与 =2矛盾,
(2) ,
又 。将上述各式两边分别相加得
点评:用放缩法证明不等式过程中,往往采用添项或减项的“添舍”放缩,拆项对比的分项放缩,函数的单调性放缩,重要不等式放缩等。放缩时要注意适度,否则不能同向传递。
【模拟试题】
1、设a、b是满足ab<0的实数,那么( )
A、 B、
C、 D、
2、设ab>0,下面四个不等式①|a+b|>|a|;②|a+b|<|b|;③|a+b|<|a-b|;④|a+b|>|a|-|b|中,正确的是( )
A、①和② B、①和③ C、①和④ D、②和④
3、下面四个式子① ;② ;③ ;④ 中,成立的有( )
A、1个 B、2个 C、3个 D、4个
4、若a、b、c∈R,且 ,则下列不等式成立的是( )
A、 B、
C、 D、
5、设a、b、c∈R,且a、b、c不全相等,则不等式 成立的一个充要条件是( )
A、a、b、c全为正数 B、a、b、c全为非负实数
C、 D、
6、已知a<0,-1<b<0则( )
A、 B、
C、 D、
7、设实数x、y满足 ,若对满足条件的x、y,x+y+c≥0恒成立,c的取值范围是( )
A、 B、
C、 D、
8、对于任意的实数x,不等式 恒成立,则实数a的取值范围是_________。
9、若a>c>b>0,则 的值的符号为__________。
10、设a、b、c∈R+,若 ,则 __________。
11、已知x,y∈R,且 ,则z的取值范围是__________。
12、设 ,
求证: 。
13、已知a、b是不等正数,且 ,
求证: 。
14、已知 ,求证: 中至少有一个不小于 。
15、设a、b为正数,求证:不等式 ①
成立的充要条件是:对于任意实数x>1,有 ②
【试题答案】
1、B 2、C 3、C 4、B 5、C 6、D 7、A
8、(-∞,3)
9、负
10、9
11、
12、证明:
13、证明:a、b是不等正数,且
而 一定成立,故 成立。
14、证明:用反证法。假设 都小于 ,则 ,
而
,相互矛盾,
中至少有一个不小于 。
15、证明:设 ,那么不等式②对 恒成立的充要条件是函数 的最小值大于b。
当且仅当 , 时,上式等号成立。
故 的最小值是 。
因此,不等式②对x>1恒成立的充要条件是 >b 。
更多阅读

八卦掌练习内功丹功 入手的基本方法
八卦掌练习内功(丹功)入手的基本方法作者:顾建强在我国以道家及武术内家拳锻炼身体,活动肢体,调整呼吸以保持健康,提高体质,袪除疾病的养生方法很多,一般称为吐纳,导引,以各种仿生肢体活动及调息为其特点。其中心目的,都是以追求袪病,健身,延年

教学设计的基本方法与步骤 教师资格证教学设计
2007-10-20 14:24:15教研中心 阅读次数:437广州市教育局教研室 吴必尊一、教学设计的基本概念教学设计是指为了达到预期的教学目标,运用系统观点和方法,遵循教学过程的基本规律,对教学活动进行系统

《谁在我家》07:系统排列的基本方法1
第七章:系统排列的基本方法家庭系统排列的过程可以分成三个阶段。在此过程中展示出家庭系统中的两种不同画面:一个是破坏性的両面,一个是解决的画面。系统排列的第一个阶段,呈现出当事人的记忆和内在的画面,那个画面展示出运作在家庭

转载 民法案例分析的基本方法探讨===案例分析法 5why分析法经典案例
原文地址:民法案例分析的基本方法探讨===案例分析法作者:老客民法案例分析的基本方法探讨王利明萨维尼曾谓:“解释法律,系法律学的开端,并为其基础,系一项科学性的工作,但又为一种艺术。”
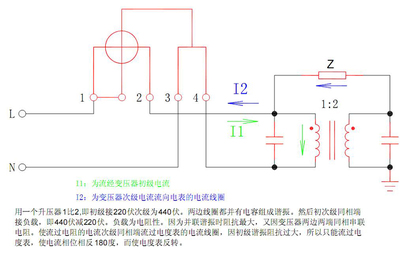
常见偷电的基本方法 脉冲电表偷电最新方法
一、欠压法偷电偷电者采用各种手法故意改变电能计量电压回路的正常接线,或故意造成计量电压回路故障,致使电能表的电压线圈失压或所受电压减少,从而导致电量少计,这种偷电方法就叫欠压偷电法。下面,我们看看欠压偷电法都有那些手法:1、使
 爱华网
爱华网