.........
V=1/2(ab+AB)h-1/6(A-a)(B-b) h
V=h/6{ab+(a+A)(b+B)+AB}
.......................
如下底1.5×1.3,上底0.4×0.4,高1.5 ,正确答案是1.435。各种体积(正方、长方、锥体、锥台体甚至圆台体)都可以!
圆台体上下底面积:∏R*R理解成边长根号∏×R的正方形
********************************************
发错了 应该是这两个公式 我算的是四棱台 网上看见了两个公式 一个是V=h/6{ab+(a+A)(b+B)+AB} 还有一个是V=1/3(S1+√S1S2+S2)h 这两算起来差不多 不过该用那个比较准确??
............................
因为(x+y)(x+y)≥2xy
所以(aA+bB)/2≥(aAbB)0.5
V=h/6(ab+AB+(A+a)(B+b))=h/3(ab+AB+(aA+bB)/2)=h/3(S1+S2+(aA+bB)/2))
≥h/3(S1+S2+(aAbB)0.5=h/3(S1+S2+(abBA)0.5=h/3(S1+S2+(S1S2)0.5
故V=h/6(ab+AB+(A+a)(B+b))比较通用,
而 V=(1/3)[S1+√(S1S2)+S2] ×h (√ 表示平方根)特例
-------------------------------------------------------
1/3*H*(S1+S2+根号S1S2)仅适用于正棱台,其他都不行,必须用1/6*H那个
***************************************************
我用拟柱体公式来解决一下,至于公式本身证明需要用到积分知识(需要同时推广牛顿-莱布尼茨公式),不详谈:
任何立体的体积均可以归纳成:
V=1/6×h×(S1+S2+4S)
S1指上表面
S2指下表面
S指高线垂直平分面
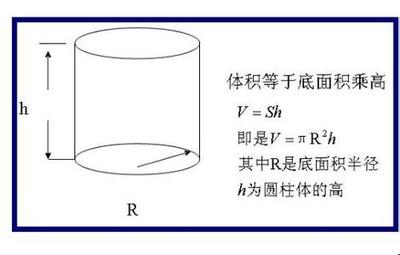
柱体:
V=1/6×h×(S1+S2+4S)
V=1/6×h×(S1+S1+4S1)
V=1/6×h×6S

V=Sh
锥体:
V=1/6×h×(S1+S2+4S)
V=1/6×h×(S2/4×4+S2)
V=1/6×h×2S2
V=1/3×S2h
球体:
V=1/6×h×(S1+S2+4S)
V=1/6×2r×(4S)
V=4/3×Sr
V=4/3兀r^3
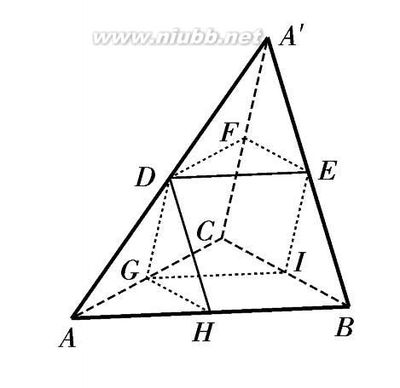
棱台:
V=1/6×h×(S1+S2+4S)
V=1/6×h×(2S1+2S2+2sqrt(S1S2))………………………(S的计算公式)
V=1/3×h×(S1+S2+sqrt(S1S2))
圆台、球冠、球缺甚至球台都可以套用这个公式,计算并不复杂,建议各位都要牢牢记住。(当然,这个公式推导过程是相当繁琐的,有机会我将专门证明这个公式。)
...........................................
一般棱台公式均要求棱台棱线延长后能交于一点,
该公式也是在这个前提下推出来的
...................
转贴----椭圆的面积和周长
椭圆的面积和周长,也是个常问问题。
面积用定积分或者拉伸变换来算吧S=πab
迄今为止高等数学也不能彻底精确地解决椭圆周长的计算问题。
以下为转贴
也有一些单位近似公式:如p=π(1.5(a+b)-√(ab))
以下是几个比较简单的近似公式:
公式一~五为一般精度,满足简单计算需要;
公式六为高精度,满足比较专业一些的计算需要。
这些公式均符合椭圆的基本规律,
当a=b时,L=2aπ,
当b=0时,L=0.
一、
L1=πQN/arctgN
(b→a、Q=a+b、N=((a-b)/a)^2、)
这是根据圆周长和割圆术原理推导的,精度一般。
二、
L2=πθ/45°(a-c+c/sinθ)
(b→0,c=√(a^2-b^2),θ=arccos((a-b)/a)^1.1、)
这是根据两对扇形组成椭圆的特点推导的,精度一般。
三、
L3=πQ(1+MN)
(Q=a+b、M=4/π-1、N=((a-b)/a)^3.3、)
这是根据圆周长公式推导的,精度一般。
四、
L4=π√(2a^2+2b^2)(1+MN)
(Q=a+b、M=2√2/π-1、N=((a-b)/a)^2.05、)
这是根据椭圆a=b时的特点推导的,精度一般。
五、
L3=√(4abπ^2+15(a-b)^2)(1+MN)
(M=4/√15-1、N=((a-b)/a)^9)
这是根据椭圆a=b,b=0时的特点推导的,精度较好。
六、
L4=πQ(1+3h/(10+√(4-3h))(1+MN)
(Q=a+b、H=((a-b)/(a+b))^2
M=22/7π-1、M=((a-b)/a)^33.697、)
这是根据椭圆标准公式提炼的,精度很高。
周长问题也可以参看
http://www.chinaai.org/down/paper/el.zip
作者:KeyTo92007-4-122:53
...........................
 爱华网
爱华网