高中数学常用公式汇总及结论 高中数学常用公式默写
2 、集合 的子集个数共有 个;真子集有 个;非空子集有个;非空的真子集有 个.
3 、二次函数的解析式的三种形式:
(1) 一般式:
(2) 顶点式 : (当已知抛物线的顶点坐标 时,设为此式)
(3) 零点式: (当已知抛物线与轴的交点坐标为 时,设为此式)
(4)切线式: 。(当已知抛物线与直线 相切且切点的横坐标为 时,
设为此式)
4、 真值表: 同真且真,同假或假
5 、常见结论的否定形式;
6 、四种命题的相互关系(下图):(原命题与逆否命题同真同假;逆命题与否命题同真同假.)
充要条件: (1) 则P是q的充分条件,反之,q是p的必要条件;
(2) 且q ≠> p,则P是q的充分不必要条件;
(3) p ≠> p ,且 ,则P是q的必要不充分条件;
(4)p ≠> p ,且 则P是q的既不充分又不必要条件。
7、 函数单调性:
增函数:(1)文字描述是:y随x的增大而增大。
(2)数学符号表述是:设f(x)在 上有定义,若对任意的 ,都有 成立,
则就叫 在上是增函数。D则就是f(x)的递增区间。
减函数:(1)、文字描述是:y随x的增大而减小。
(2)、数学符号表述是:设f(x)在xD上有定义,若对任意的 ,都有
成立,则就叫f(x)在上是减函数。D则就是f(x)的递减区间。
单调性性质:(1)、增函数+增函数=增函数; (2)、减函数+减函数=减函数;
(3)、增函数-减函数=增函数; (4)、减函数-增函数=减函数;
注:上述结果中的函数的定义域一般情况下是要变的,是等号左边两个函数定义域的交集。
复合函数的单调性:
等价关系:
(1)设 ,那么
上是增函数;
上是减函数.
(2)设函数 在某个区间内可导,如果 ,则 为增函数;如果 ,则为减函 数.
8、函数的奇偶性:(注:是奇偶函数的前提条件是:定义域必须关于原点对称)
奇函数定义:在前提条件下,若有 , 则f(x)就是奇函数。
性质:(1)、奇函数的图象关于原点对称;
(2)、奇函数在x>0和x<0上具有相同的单调区间;
(3)、定义在R上的奇函数,有f(0)=0 .
偶函数定义:在前提条件下,若有f(—x)=f(x),则f(x)就是偶函数。
性质:(1)、偶函数的图象关于y轴对称;
(2)、偶函数在x>0和x<0上具有相反的单调区间;
奇偶函数间的关系:
(1)、奇函数·偶函数=奇函数; (2)、奇函数·奇函数=偶函数;
(3)、偶奇函数·偶函数=偶函数; (4)、奇函数±奇函数=奇函数(也有例外得偶函数的)
(5)、偶函数±偶函数=偶函数; (6)、奇函数±偶函数=非奇非偶函数
奇函数的图象关于原点对称,偶函数的图象关于y轴对称;反过来,如果一个函数的图象关于原点对称,
那么这个函数是奇函数;如果一个函数的图象关于y轴对称,那么这个函数是偶函数.
9、函数的周期性: 定义:对函数f(x),若存在 ,使得f(x+T)=f(x),则就叫f(x)是周期函数,
其中,T是f(x)的一个周期。
周期函数几种常见的表述形式:
(1)、 f(x+T)= - f(x),此时周期为2T ;
(2)、 f(x+m)=f(x+n),此时周期为 ;
(3)、 此时期为2m 。
10、常见函数的图像:
11、 对于函数 恒成立,则函数的对称轴是 ;
两个函数f=(x+a)与y=(b-x) 的图象关于直线 对称.
12、 分数指数幂与根式的性质:
13 、指数式与对数式的互化式: .
指数性质:
指数函数:
(1)、 在定义域内是单调递增函数;
(2)、 在定义域内是单调递减函数。注: 指数函数图象都恒过点(0,1)
对数性质:
对数函数:
(1)、 在定义域内是单调递增函数;
(2)、 在定义域内是单调递减函数;注: 对数函数图象都恒过点(1,0)
(3)、
(4)、
14、 对数的换底公式 :
对数恒等式
推论
15、对数的四则运算法则:若a>0,a≠1,M>0,N>0,则
16、 平均增长率的问题(负增长时):如果原来产值的基础数为N,平均增长率为p,则对于时间的总产值,
有 .
17 、等差数列:通项公式: (1) ,其中 为首项,d为公差,n为项数, 为末项。
(2)推广:
(3) (注:该公式对任意数列都适用)
前n项和: (1) ;其中为首项,n为项数,为末项。
(2)
(3) (注:该公式对任意数列都适用)
(4) (注:该公式对任意数列都适用)
常用性质:(1)、若m+n=p+q ,则有 ;
注:若 的等差中项,则有 n、m、p成等差。
(2)、若 、为等差数列,则 为等差数列。
(3)、 为等差数列,为其前n项和,则 也成等差数列。
(4)、
(5)
等比数列:
通项公式:(1) ,其中为首项,n为项数,q为公比。
(2)推广 :
(3) (注:该公式对任意数列都适用)
前n项和:(1) (注:该公式对任意数列都适用)
(2) (注:该公式对任意数列都适用)
(3)
常用性质: (1)、若m+n=p+q ,则有 ;
注:若 的等比中项,则有 成等比。
(2)、若、 为等比数列,则 为等比数列。
18、分期付款(按揭贷款) :每次还款 元(贷款元,次还清,每期利率为).
19、三角不等式:
(1)若 ,则 .
(2) 若 ,则 .
(3) .
20 、同角三角函数的基本关系式 :
21、 正弦、余弦的诱导公式(奇变偶不变,符号看象限)
22、 和角与差角公式
(辅助角 所在象限由点(a,b) 的象限决定 , ).
23、 二倍角公式及降幂公式
.
24、 三角函数的周期公式
函数 及函数 ),x∈R(A,ω,为常数,且A≠0)的周期 ; 函数,(A,ω,为常数,且A≠0)的周期 .
三角函数的图像:
25 、正弦定理 : (R为 外接圆的半径).
26、余弦定理:
27、面积定理:
(1) 分别表示a、b、c边上的高).
28、三角形内角和定理 :
在△ABC中,有
.
29、实数与向量的积的运算律:设λ、μ为实数,那么:
30、与的数量积(或内积): ·
31、平面向量的坐标运算:
32 、两向量的夹角公式:
33、 平面两点间的距离公式:
34、 向量的平行与垂直 :设=,=, ,则:
(交叉相乘差为零)
(对应相乘和为零)
35 、线段的定比分公式 :设 ,是线段 的分点,是 实数,
且 ,则
36、三角形的重心坐标公式: 三个顶点的坐标分别为
则的重心的坐标是
.
37、三角形五“心”向量形式的充要条件:设为所在平面上一点,角所对边长分别为,则
38、常用不等式:
39、极值定理:已知都是正数,则有
(1)若xy积是定值P,则当x=y时和有最小值 ;
(2)若x+y和是定值S,则当x=y时积有xy最大值 .
(3)已知 ,若 则有
(4)已知 ,若则有
40、 一元二次不等式 ,如果a与 同号,则其解集在两根之外;如果a与 异号,则其解集在两根之间.简言之:同号两根之外,异号两根之间.即:
.
41 、含有绝对值的不等式 :当a> 0时,有
.
42、 斜率公式 :
43 、直线的五种方程:
(1)点斜式: (直线 ).
(2)斜截式: (b为直线在y轴上的截距).
(3)两点式:
两点式的推广: (无任何限制条件!)
(4)截距式 : (分别为直线的横、纵截距, )
(5)一般式: (其中A、B不同时为0).
直线的 法向量: ,方向向量 :
44 、夹角公式:
45 、到的角公式:
46、 点到直线的距离 : (点,直线:).
47、 圆的四种方程:
(1)圆的标准方程 :
(2)圆的一般方程: (>0).
(3)圆的参数方程 :
(4)圆的直径式方程 : (圆的直径的端点是
48、点与圆的位置关系:点 与圆 的位置关系有三种:
若
49、直线与圆的位置关系:直线 与 圆的位置关系有三种
50 、两圆位置关系的判定方法:设两圆圆心分别为O1,O2,半径分别为r1,r2,, 则:
.
51 、椭圆 的参数方程是 . 离心率 ,
准线到中心的距离为 ,焦点到对应准线的距离(焦准距) 。
过焦点且垂直于长轴的弦叫通经,其长度为 :.
52、 椭圆 焦半径公式及两焦半径与焦距构成三角形的面积:
53、椭圆的的内外部 :
54、椭圆的切线方程:
55 、双曲线的 离 心率 ,准线到中心的距离为 ,焦点到对应准线的距离(焦准距) 。过焦点且垂直于实轴的弦叫通经,其长度为:.
焦半径公式 ,
两焦半径与焦距构成三角形的面积 。
56 、双曲线的方程与渐近线方程的关系:
(1)若双曲线方程为 渐近线方程:
(2)若渐近线方程为 双曲线可设为.
(3)若双曲线 与有公共渐近线,可设为
( ,焦点在x轴上, ,焦点在y轴上).
(4) 焦点到渐近线的距离总是b。
57、双曲线的切线方程:
.
58、抛物线 的焦半径公式:
抛物线 焦半径
过焦点弦长 .
59、二次函数 的图象是抛物线:
(1)顶点坐标为 ;(2)焦点的坐标为 ;
(3)准线方程是
60 、直线与圆锥曲线相交的弦长公式 :
或
(弦端点 ,由方程 消去y得到
为直线的倾斜角, 为直线的斜率
61、证明直线与平面的平行的思考途径:
(1)转化为直线与平面无公共点;
(2)转化为线线平行;
(3)转化为面面平行.
62、证明直线与平面垂直的思考途径:
(1)转化为该直线与平面内任一直线垂直;
(2)转化为该直线与平面内相交二直线垂直;
(3)转化为该直线与平面的一条垂线平行;
(4)转化为该直线垂直于另一个平行平面。
63、证明平面与平面的垂直的思考途径:
(1)转化为判断二面角是直二面角;
(2)转化为线面垂直;
(3) 转化为两平面的法向量平行。
64、 向量的直角坐标运算:
65、 夹角公式:
设 则
66 、异面直线间的距离 :
( 是两异面直线,其公垂向量为 ,C,D是 上任一点,d为 间的距离).
67、点到平面 的距离: ( 为平面的法向量,, 是的一条斜线段).
68、球的半径是R,则其体积 ,其表面积 .
69、球的组合体:
(1)球与长方体的组合体: 长方体的外接球的直径是长方体的体对角线长.
(2)球与正方体的组合体:正方体的内切球的直径是正方体的棱长, 正方体的棱切球的直径是正方体的面对角线长,
正方体的外接球的直径是正方体的体对角线长.
(3)球与正四面体的组合体: 棱长为 的正四面体的内切球的半径为
(正四面体高 ,外接球的半径为 (正四面体高
70 、分类计数原理(加法原理): .
分步计数原理(乘法原理): .
71、排列数公式 :
72 组合数公式:
组合数的两个性质:
73 、二项式定理:
二项展开式的通项公式:
的展开式的系数关系:
74 、互斥事件A,B分别发生的概率的和:P(A+B)=P(A)+P(B).
个互斥事件分别发生的概率的和:P(A1+A2+…+An)=P(A1)+P(A2)+…+P(An).
75 、独立事件A,B同时发生的概率:P(A·B)= P(A)·P(B).
n个独立事件同时发生的概率:P(A1· A2·…· An)=P(A1)· P(A2)·…· P(An).
76、 n次独立重复试验中某事件恰好发生k次的概率:
77、 数学期望:
数学期望的性质
(1).
(2)若 则 .
(3) 若 服从几何分布,且
78、方差:
标准差:
方差的性质:
(1);
(2)若
(3) 若 服从几何分布,且
方差与期望的关系:
79、正态分布密度函数:
式中的实数 是参数,分别表示个体的平均数与标准差.
对于 ,取值小于x的概率: .
80 、 处的导数(或变化率):
.
81 、函数 在点 处的导数的几何意义:
函数 在点处的导数是曲线 在处的切线的斜率 ,相应的切线方程是 .
82、几种常见函数的导数:
83、 导数的运算法则:
84、 判别 是极大(小)值的方法:
当函数f(x)在点处连续时,
85 、复数的相等:
86、 复数 的模(或绝对值)
87、 复平面上的两点间的距离公式:
88、实系数一元二次方程的解
实系数一元二次方程
③若 ,它在实数集内没有实数根;在复数集内有且仅有两个共轭复数根.
更多阅读
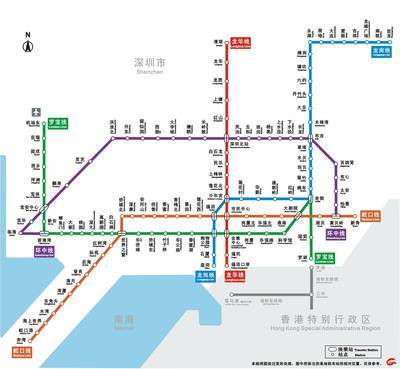
北京地铁线路图汇总及未来规划和在建地铁线路图 深圳未来地铁线路图
北京地铁线路图汇总及未来规划和在建地铁线路(图)关键词:北京地铁,地铁线路 北京地铁站真的变化很大,由原来的1号线,2号线,和八通线增加到现在的4号,5号,8号,9号线,10号,13号等多条线路,可以说是四通八达,东南西北,人们可以从北五环,直接到南
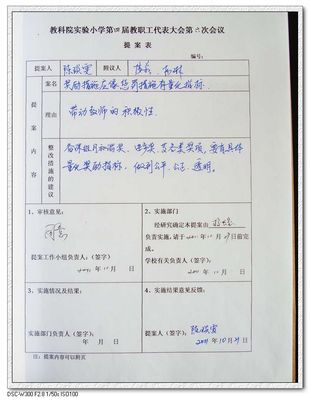
教代会提案汇总及答复 教代会提案表范文
(2010-12-17 11:23:57) 转载▼标签: 教代会提案答复关注学校发展杂谈分类: 随笔今天下午,我们召开了本校第一届一次全体教工代表大会。会上选举产生了校工会委员,通过几项决议。以下是针对代表提案,代表学校作出的答复。尊敬的县教体局X

高中数学常用公式及结论2 高中数学竞赛常用公式
41 含有绝对值的不等式 :当a> 0时,有 . 或 .42 斜率公式 : ( 、 ).43 直线的五种方程:(1)点斜式 (直线 过点 ,且斜率为 ).(2)斜截式 (b为直线 在y轴上的截距).(3)两点式 ( )( 、 ( )).两点式
“数量关系”常用数学公式汇总系统版 信号与系统常用公式
“数量关系”常用数学公式汇总一、(2、4、8)整除及余数判定基本法则一个数能被2(或5)整除,当且仅当其末一位数能被2(或5)整除;一个数能被4(或25)整除,当且仅当其末两位数能被4(或25)整除;一个是能被8(或125)整除,当且仅当其末三位数能被8(或125)整
高中数学常用公式及结论 高中数学常用二级结论
1元素与集合的关系: , .2集合 的子集个数共有 个;真子集有 个;非空子集有 个;非空的真子集有 个.3二次函数的解析式的三种形式:(1)一般式 ;(2)顶点式 ;(当已知抛物线的顶点坐标 时,设为此式)(3)零点式 ;(当
 爱华网
爱华网