离散数学复习
1The Foundations: Logic and Proofs(逻辑与证明)
1.1Propositional Logic(命题逻辑)
Propositions(命题)——declarative sentence that is either true orfalse, but not both.判断性语句,正确性唯一。
Truth Table(真值表)
Conjunction(合取,“与”,and),Disjunction(析取,or,“相容或”),Exclusive(异或),Negation(非,not),Biconditional(双条件,双向,ifand only if)
Translating English Sentences
1.2Propositional Equivalences(命题等价)
Tautology(永真式、重言式),Contradiction(永假式、矛盾式),Contingency(偶然式)
Logical Equivalences(逻辑等价)——Compound propositions that have thesame truth values in all possible cases are called logicalequivalent.(真值表相同的式子,p<->q是重言式)
Logical Equivalences——Page24
Disjunctive normal form(DNF,析取范式)
Conjunctive normal form(CNF,合取范式) 见Page27~29
1.3Predicates and Quantifiers(谓词和量词)
Predicates——谓词,说明关系、特征的修饰词
Quantifiers——量词
Ø Universal Quantifier(全称量词)"
全部满足
Ø ExistentialQuantifier(存在量词)$
至少有一个
Binding Variables(变量绑定,量词作用域与重名的问题)
Logical Equivalence Involving Quantifiers
Negating Quantified Expressions(量词否定表达:否定全称=存在否定,否定存在=全程否定)
Translating from English into Logical Expressions(自然语句转化为逻辑表达)
Using Quantifiers in System Specifications
Examples from LewisCarrol——全称量词与条件式(p->q)搭配,存在量词与合取式搭配。
1.4Nested Quantifiers(量词嵌套)Page5912、13
"x"yP(x,y) Û "y "x P(x,y)
$x $yP(x,y) Û $y$xP(x,y)
"x"yP(x,y) Þ $y"xP(x,y)
"y"xP(x,y) Þ $x"yP(x,y)
$x"yP(x,y) Þ "y$xP(x,y)
$y"xP(x,y) Þ "x$yP(x,y)
"x$yP(x,y) Þ $y$xP(x,y)
"y$xP(x,y) Þ$x$yP(x,y)
Prenex normal form(PNF前束范式):所有量词变换到最前面,否定变换到后面。
1.5Rules of Inference(推理规则)
Valid Arguments in Propositionnal Logic(命题逻辑中的正确论点)
Premises(前提)——all but the final proposition in the argument

Conclusion(结论)
Rules of Inference for Propositionnal Logic
Page 66~67,证明方法及过程示范
Resolution(归结): ((p∨q) ∧(┐p ∨r)) →(q ∨ r) 合取,若两子句有互补文字,则可消去。
Fallacies(谬论)
Rules of Inference for Quantified Statements
Universal instantiation(全称量词实例化)
Universal generalization(全称量词一般化)
Existential instantiation(存在量词实例化)
Existential generalization(存在量词一般化) Page70
以上四点,其实就是一般和特殊之间的转换。名字是骗人的。
1.6Introduction to Proofs
Direct proof:证明p->q
Proof by Contraposition:对位证明,通过证明其逆反命题来证明原命题
Vacuous and Trivial Proofs
Proof by Contradiction:反证法
1.7Proof Methods and Strategy
2Basic Structures: Sets, Functions, Sequences andSums(集合、函数、序列与和)
Cardinality 集合的势,即其中元素的个数。
Power Set :the set of all subsets of the setS.原集合的所有子集组成的集合。
Cartesian product:笛卡尔积、直积,A×B={(a,b)|a∈A∧b∈B}
Function
Onto:满射
Injective=One-to-One:单射
Bijection:双射=单射加满射
3~7 略
8Relations(关系)
8.1 relations and Their Properties
Reflecxive自反:if (a, a)∈R for every element a∈A 都有环
Irreflexive 反自反:一个环也没有
Symmetric 对称:if (b, a)∈R whenever (a, b)∈R, for alla,b.有从a到b,必有从b到a。
Antisymmetric 反对称:除非a=b,有从a到b,必无从b到a。
Asymmetric 不对称:有从a到b,必无从b到a。
Transitive 传递:a到b,b到c,则有a到c。
CombiningRelations(复合关系):S·R(空心圆圈)
分配率:并集满足等价,交集满足包含
(1) Fo(GÈH)= FoG È FoH
(2) Fo(GÇH)Í FoGÇ FoH
(3) (GÈH) oF = (GoF ) È (HoF)
(4) (GÇH) oFÍ GoFÇ HoF
Rn + 1= Rn oR
The relation R on a set A is transitive if and only ifRn属于R for n=1,2,3……
8.2 n-ary Relations and Their Applications
8.3 Representing Relations(表示关系)
Ø Representing Relations UsingMatrices——Zero-One Matrix
Reflexive自反:主对角线上的数都为1。
Symmetric对称:以主对角线为轴对称。
Ø Representing Relations UsingDigraphs(有向图)
8.4 Closures of Relations(关系的闭包)
闭包是指在原关系的基础上添加最少的有序对,构成满足一种特性的新的关系。自反闭包、对称闭包和传递闭包。
Reflexive closure(自反闭包):在所有元素上加环。
Symmetric closure(对称闭包):对于所有的(a, b),添加(b, a)。
Transitive Closure(传递闭包):⊙:先合取再析取
M(R*)=M(R)∨(M (R)∧M(R))∨(M(R)∧M(R)∧M(R))……直到第n项
*Warshall’s Algorithm沃舍尔算法
8.5 Equivalence Relations
A relation on a set A is called an equivalence relation if it isreflexive, symmetric, and transitive.
等价=自反+对称+传递
A的全域关系和恒等关系都是等价关系,空关系不具自反性。
² 全域关系:全部有序偶。
² 恒等关系:对称且反对称,有且只能有环。
Equivalent等价量
Equivalence Classes等价类
集合中具有等价关系的一个子集。集合中与一个元素具有等价关系的全部元素构成的子集。
Partitions分割
² 非空、无交集、其并集为全集。
² Let R be an equivalence relation on a set S.Then the equivalence classes of R form a partition of S.Conversely, given a partition {Ai | i ∈I} of the set S, there is anequivalence relation R that has the sets Ai, i∈I, as itsequivalence classes.
8.6 Partial Orderings偏序关系
A relation R on a set S is called a partial ordering or partialorder if it is reflexive, antisymmetric, and transitive. A set Stogether with a partial ordering R is called a partially orderedset, or poset, and is denoted by (S, R).
自反+反对称+传递
Comparable可比:The elements a and b of a poset (S,*)are called comparable if either a*b or b*a.
Totally ordered or linearlyordered(全序或线序):没两个元素都是可比的。这样的集合又称作链(chain)
Lexicographic Order(字典序) Page 569
Well-ordered(良序):A chain (A, R) iswell-ordered良序 iff every nonemptysubset of A has a least element.
HasseDiagrams(哈斯图)
To construct a Hasse diagram:
1) Construct a digraph representation of the poset (A, R)so that all arcs point up (except the loops).(所有的弧指向上)
2) Eliminate all loops(删除环)
3) Eliminate all arcs that are redundant because oftransitivity(删除由于传递而多余的弧)
4) Eliminate the arrows at the ends of arcs since everythingpoints up.(删除箭头)
Maximal and Minimal Elements
Great and Least Element(唯一)
Upper and Lower Bounds
Least Upper and Greatest LowerBound(唯一)Page 572~574
Lattices格
对于一个偏序集A,若其中任意两个元素a、b,都有最大下界和最小上界,则称这样的偏序集为格。
Topological Sorting拓扑排序
Not only one possible order.可能有多种排序方式。
9 Graphs(图论)
9.1 Graphs and Graph Models
Type | Edges | Multiple Edges Allowed | Loops Allowed |
Simple graph简单图 | Undirected | No | No |
Multigraph多重图 | Undirected | Yes | No |
Pseudograph伪图 | Undirected | Yes | Yes |
Simple directed graph简单有向图 | Directed | No | No |
Directed multigraph多重有向图 | Directed | Yes | Yes |
Mixed graph混合图 | Both | Yes | Yes |
简单图+多重边——>重图,重图+环——>伪图
Graph Models
Page 592~595
9.2 Graph Terminology and Special Types ofGraphs(图论术语和特殊图)
Adjacent andIncident(连接和关联):一条边相连的两点为连接,该边与这两点关联。这两点称作端点(endpoints).
Degree:度,与一个点相关联的边数,deg(v).
Isolated Vertex:孤立点,dev(v)=0.
Pendant Vertex:悬挂点,dev(v)=1.
The Handshaking Theorem(握手定理)
Let G=(V,E) be an undirected graph withe edges. Then 2e=∑deg(v).
度数是边数的两倍。
An undirected graph has an even number of vertices of odddegree.奇数度顶点有偶数个。
In-degree(入度): deg-(v),the number of edges with v astheir terminal vertex(终点).
Out-degree(出度):deg+(v), the number ofedges with v as their initial vertex(起点).
Let G=(V, E) be a graph with directed edges.Then∑deg-(v)=∑deg+(v)=|E|.
Some Special Simple Graphs
Complete Graphs(全图) is the Simplegraph that contains exactly one edge between each pair ofdistinct vertices. Kn 顶点数:n,边数:n(n+1)/2.
Cycles(圈图),Cn 顶点数n,边数n.
Wheels(轮图),Wn 顶点数n+1, 边数2n.
Cube(方图),Qn 顶点数2n,边数2n-1*n
Bipartite Graphs(偶图,二分图)
可通过着色法判断,有边相连的两点颜色不同,总共只有两种颜色。
Complete Bipartite Graphs(完全二分图)
New Graphs from Old——Subgraph(子图)
Ø 生成子图Spanning Subgraph:与原图顶点相同,边是真子集。
Ø 导出子图:顶点是原图顶点的子集,而边为与它们相连的原图的所有边。
The union of the simple graphs:所有简单图的边与顶点的并集所得到的简单图。
9.3 Representing Graphs and GraphIsomorphism(图的表示与同构)
Adjacency Lists and Matrices(邻接表与邻接矩阵) Page612 点与点的关系
对于有向图的邻接矩阵,行数字相加为该点出度,列数字相加为该点入度,所有数字相加为度数的一半,即边数。
Incidence Matrices(关联矩阵)点与边的关系。
Isomorphism of Graphs(图的同构)
必要条件:
1,相同顶点数
2,相同的边数
3,对应顶点的度数相同
4,子图相同
5,路径相同
使用矩阵判断两图是否同构:
Ø 邻接矩阵:任意交换行列,调整至两矩阵相同,即为同构。
Ø 关联矩阵:行与对应列同时做相同变动,调整至两矩阵相同,为同构。
9.4 Connectivity连通
Paths(路径)——有向图路径和无向图路径
Circuit(回路),Traverse(遍历)
简单路径:每条边只出现一次。
初级路径:每个点只出现一次。
Connectedness in UndirectedGraphs(无向图的连通)
An undirected graph is called connected if there is a pathbetween every pair of distinct vertices of the graph.
Connected component 连通分支:Maximalconnected subgraph of G.
Cut vertices(割点)/cut edge(割边、或bridge桥):扔掉它们就会产生更多连通分支的东西。
Connectedness in Directed Graphs
Strongly connected强连通——路径a到b和b到a同时存在。
Weakly connected弱连通——两点之间有线存在(underlying undirectedgraph看作无向图路径即可)。
强连通一定是弱连通。
Counting Paths between Vertices
使用该图的邻接矩阵A,长度为n,就计算An。对应行乘以对应列。
The (i, j)th entry of Ar+1 equals:bi1a1j+bi2a2j+bi3a3j+…+binanj.
9.5 Euler and Hamilton Paths
Ø Euler Paths andCircuits:欧拉路径、回路,周游原图的每一条边。
Ø Hamilton Paths andCircuits:哈密顿路径、回路,周游每个顶点。
² 一个连通重图具有欧拉回路,当且仅当它的每个顶点都是偶数度。
² 一个连通重图具有欧拉路径(称为半欧拉图),当且仅当它有且只有两个奇度数顶点。
对于一个有向图而言:
欧拉回路的条件:
1,每个顶点都有偶数度。
2,出度等于入度。
欧拉路径的条件:
1,仅有两个顶点有奇数度。
2,对于偶度数顶点,出度等于入度。
3,对于奇数度顶点,出度和等于入度和。
Hamilton Paths and Circuits
充分条件:
Ore’s Theorem: If G is a simplegraph with n vertices with n≥3 such that deg(u)+deg(v)≥n forevery pair of nonadjacent vertices u and v in G, then G has aHamilton circuit.任意两顶点度数之和不小于总的顶点数。
Dirac’s Theorem: If G is a simple graph with n verticeswith n≥3 such that the degree of every vertex is at least n/2, thenG has a Hamilton circuit.每一点的度数都不小于总顶点数的一半。
必要条件:
If G is a Hamiltonian graph, then for every nonempty proper setS of vertices of G, K(G-S)≤|S|.删去任意顶点后的连通分支数不大于删去的顶点数。
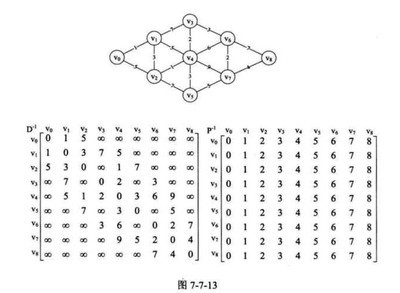
9.6 Shortest-Path Problems
Weighted graphs(带权图)——边带权和顶点带权。
A Shortest-Path Algorithm
The Traveling Salesman Problem
9.7 Planar Graphs
定义:可以画在一个平面内,而没有任意两条边交叉的图。
最小非平面图:删去一条边可以变成平面图的非平面图。
最大平面图:任意加一条边都会变成非平面图的平面图。
Euler’s Formula 平面图欧拉公式
Region=edge-vertice+2 (connected planarsimple graph平面连通简单图)
所有面的度数之和等于边数的两倍。
区域度数计算:围成该区域的边数,悬挂边记作两度。
Corollary 1:If G is a connected planar simple graph with e edgesand v vertices, where v≥3, then e≤3v-6.
Corollary 2:If G is a connected planar simple graph, then G hasa vertex of degree not exceeding five.
Kuratowski’sTheorem(库拉图斯基/苦辣兔斯基定理)
Elementarysubdivision(初等分割)&Homeomorphic(同胚)
增加新的点只能是有两度的点,删点也只能删两度的点。
‘K’ Theorem: A graph is nonplanar if and only if itcontains a subgraph homoeomorphic to K3,3 orK5.
9.8 Graph Coloring
DualGraph——对偶图:指原图中的每个封闭区域对应一个点,每条边对应一条边(连接两顶点,与原来的边相交)而形成的新图。环对应悬挂边。
同构的图,对偶图不一定同构。
Chromatic Number(色数):为一个图上色所需的最少颜色数。
The Four Color Theorem: The chromatic number of a planargraph is no greater than four.
10 Trees(树)
10.1 Introduction to Trees
Definition: a tree is a connected undirected graphwith no simple circuits.
An undirected graph is a tree if and only if there is a uniquesimple path between any two of its vertices. (任意两点之间只有一条通路)
A rooted tree(根树) is a tree in which one vertex has beendesignated as the root and every edge is directed away from theroot.
Internal vertices: vertices that havechildren.(有子节点的节点)
Leaf,leaves:vertices that have nochildren.(末节点)
m-ary tree(m元树):每一批孩子都不多于m个的树。
Full m-ary tree(完全m元树、完全正则树):每一批孩子都是m个的树。
Ordered rooted tree
Properties of Trees
A tree with n vertices has n-1 edges.
A full m-ary tree with i internal verticescontains n=mi+1 vertices
A full m-ary tree with
1)n vertices has i=(n-1)/m internal vertices and l=[(m-1)i+1]/mleaves.
2)i internal vertices has n=mi+1 vertices and l=(m-1)i+1 leaves.
3)l leaves has n=(ml-1)/(m-1) internal vertices.
There areat most mh leaves in an m-ary tree of heighth.
10.2 Applications of Trees
10.3 Tree Traversal
先序遍历:
中序遍历:
后序遍历:
10.4 Spanning Trees(生成树)
A spanning tree of G is a subgraph of g that is a treecontaining every vertex of G.
A spanning tree is connected if and only if it has aspanning tree.
Depth-First Search深度优先搜索
Breadth-First Search宽度优先搜索
10.5 Minimum Spanning Trees
 爱华网
爱华网