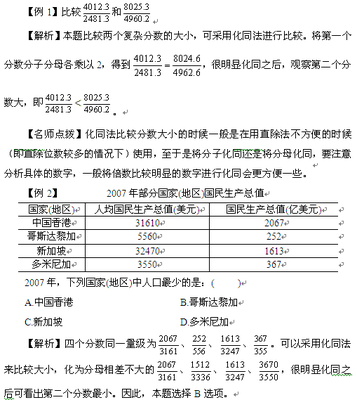
中位数即为数列的平均数。
自然数列的中位数特性:1、位置特性:一定在数列的最中间位置。2、数值特性:为整数或者为:X.5.计算方法: a中=(a1+an)÷2
下面以例题来说明中位数是如何运用的。
2008年中央国家机关公务员考试真题小华在练习自然数求和,从1开始,数着数着他发现自己重复数了一个数。在这种情况下,他将所数的全部数求平均数,结果为7.4,请问他重复的那个数是:A.2 B.6 C.8 D.10
平均数为7.4显然不符合自然数列的中位数规则。那么这个自然数列的中位数可能是7.5,即1—14的平均数,1—14的和为105。由于中间重复数了一个数字,那么他数了15个数,此时的数列和为7.4×15=111。所以小华数重复的数字为111-105=6。
数学算式——结合律法
在公务员考试中常常会出现计算一个数学算式结果的题目。这类题目往往被考生朋友视作鸡肋——弃之可惜,食之无味——本来很简单不愿放弃,但要计算又很花时间。其实在公务员考试中,由于题量大,所以所有的题目都是可以凭借解答技巧来快速作答的。算式计算当然也不例外,如下题:
1+2-3-4+5+6-7-8+9+10-11-12+…+1993+1994-1995-1996+1997+1998=?
“暴力”计算本题无疑是很大的工作量,如果我们换个角度来看这一列数字就会发现其实隐含在其中的规律。技巧1:原式可写为1+(2-3-4+5)+(6-7-8+9)+…+(1994-1995-1996+1997)+1998=?
我们可以发现所有括号内的运算结果均为0,那么最终结果就为1+1998=1999。这是顺序不变的结合。
技巧2:原式可写为(1+1998)+(2+1997)+(-3-1996)+(-4-1995)+…=?
可以发现整个算式及为1999+1999-1999-1999+…这样循环的,那么最后剩下的是0呢?还是其他组合呢?每8个数字的和为0,计算1998÷8=249…6,那么最后剩下的就是1999+1999-1999=1999,得出最终答案。
由上例我们看到灵活运用换位的及不换位的结合率可以极大的减化运算过程,节省作答时间。
结果验算——尾数法
尾数法是大家比较熟悉的一种方法。大多数人都将其看做一种计算技巧,而从其作用机理上来看它本质上实为一种应试作答技巧,因为应用尾数法无法得到一个准确的数值,而是需要对选项进行比对从而得到答案。故此尾数法在速算当中更多的是用于验证计算结果的正确性。公务员考试中的数学运算部分就全部为验证计算结果的题目,所以熟练运用尾数法是可以使我们的作答事半功倍的。
如下题:1+2+3+4+……+n=2005003,则自然数n=
A.2000 B.2001C.2002 D.2003
此题为自然数列求和,给出了数列和要求出n。那么应用等差数列求和公式【等差数列基本公式: 末项=首项+(项数-1)×公差; 项数=(末项-首项)÷公差+1 ;首项=末项-(项数-1)×公差; 和=(首项+末项)×项数÷2 ;注:末项:最后一位数;首项:第一位数;项数:一共有几位数 ;和:求一共数的总和】可得,(1+n)×n÷2=2005003,则(n+1)n=4005006。这里我们如果直接应用方程求解,无疑会非常麻烦,所以我们看一下尾数。对比选项,发现只有(2002+1)×2002的尾数为6,故答案为C。
在遇到数字偏大、运算量过大的题目时,适时适当的运用尾数法能极大的简化运算过程。
数学算式——整体代换法
注意下面的算式
如果我们运用正常的计算方法来进行计算的话,恐怕得用上5分钟左右,而公务员考试行测试卷的要求为120分钟作答140道题目!每道题目要把时间控制在1分钟之内!任务如此艰巨,我们应该如何完成?整体代换法应运而生。对于这类计算题不要急于进行“暴力”计算,首先观察所求的式子,尽量多的找出其中的同类项,把同类作为一个整体参与计算,得到最简式后再将进行替换求解,可省下不少时间。
约略比较——缩放法
大多数同学碰到这种题目的第一反应都会是:无法解答。确实对于我们来说整数的等差数列计算是很简单的,但要求分母成等差数列的分数和就完全找不到头绪了。那么我们可以运用缩放法来进行解决。
数学运算——核心考点部分
专题一 计算问题
■常见题型:
计算表达式的值、求解方程、乘方尾数问题、比较大小问题、新定义运算符号问题等
■常用技巧:
尾数法、估算法、凑整法、整体消去法、分组计算法、裂项相消法等
专题二 等差数列
■核心知识:
求和公式:和=平均数×项数=中位数×项数
项数公式:项数= +1
常用性质:等差数列 中,若 ,则 。
■常见题型:
1. 已知某些项的和,求数列中某项的值。
2. 计算某等差数列的和
3. 已知几个连续数字的乘积,求这几个数字
■解题思路:
1. 熟悉等差数列求和公式,特别注意利用和与平均数(中位数)的相互转化
2. 整数型等差数列中,连续奇数项的和一定能被项数整除。?
专题三 多位数相关问题
■核心知识:
一位数为1~9,两位数为10~99(共90个),三位数为100~999(共900个),…
■常见题型:
1. 给出数字变化过程,求取原多位数
2. 给定数字,构造符合条件的多位数
3. 与书的页码结合,考查相关问题
■解题思路:
1. 直接代入法是常用技巧。
2. 构造多位数时,注意若数字要尽可能大,则将大的数字放在高数位,将小的数字放在低数位;若数字要尽可能小,则将小的数字放在低数位,大的数字放在高数位。同时注意最高位不能放0。
专题四 余数相关问题
■核心知识:
余数基本关系式:被除数÷除数=商…余数(0≤余数<除数)
余数基本恒等式:被除数=除数×商+余数
余数常用不等式:被除数≥除数×商>余数×商
■常见题型:
1. 基本余数问题:涉及被除数、除数、商、余数中的若干量,求取其余的量。
2. 同余问题:给出一个数除以几个不同的数的余数,反求这个数。
注:上述两类问题的区别在于,基本余数问题中会涉及“商”,而同余问题则不涉及“商”。
■解题思路:
1. 基本余数问题:题目通常会告知被除数、除数、商及余数这四个量中的两个量,让求取其余两个量。此时设两个待求量,根据题目条件可以得到一个方程,根据余数基本恒等式可以再得到一个方程,联立求解即可。
2. 同余问题:解题关键是写出被除数的表达式。题目给出的条件若满足余数相同,则被除数表示为“除数的最小公倍数×n+余数”;若满足除数与余数的和相同,则被除数表示为“除数的最小公倍数×n+余数除数之和”;若满足除数与余数的差相同,则被除数表示为“除数的最小公倍数×n-除数余数之差”。
3. 基本余数问题中,若待求量为被除数,则可以先根据余数常用不等式排除不符合范围的选项;同余问题中,若待求被除数为一确定值,则一般用直接代入法。
专题五 星期日期问题
■核心知识:
1. 闰年核算:若年份不是100的倍数,则能被4整除者为闰年;若年份是100的倍数,能被400整除者为闰年。
注:这个计法严格来说并不严谨,但对考试而言已经足够了。
2. 平年365天是52周余1天,闰年366天是52周余2天。
3. 大月有一、三、五、七、八、十、十二月,每月31天,是4周余3天;小月为二、四、六、九、十一月,除二月外,每月30天,是4周余2天。二月平年为28天,恰好是4周,闰年为29天,是4周余1天。
4. 每隔N天即等价于每N+1天。
5. 核心口诀:一年就是1,闰日再加1。
解释:如果月份、日期不变,在原来的基础上加上(或减去)一年,则在原来的星期数基础上增加(或减去)“1”,如果中间有闰日,还要再加“1”。
■常见题型:
1. ××××年×月×日是星期×,则××××年×月×日是星期几?
例:2009年6月1日是星期一,那么2014年6月1日是星期几?
2. 给出今天之前(或之后)×天之后是星期×,求之前(或之后)×天是星期几?
例:今天的前5天是星期二,那么明天的前4天是星期几?
■解题思路:
1. 对第一种题型,借助口诀“一年就是1,闰日再加1”快速求解。
2. 从给出星期的那一天逐步推至待求的那一天,在这过程中,将星期数与移动天数直接相加(或减),然后除以7看余数,余几就是星期几。相加减的原则是:向未来移动,则星期数与天数相加;向过去移动,则星期数与天数相减。
专题六 平均数问题
■核心公式:
总和=平均数×个数
■常见题型:
给出多个关于某些量的平均数的条件,求取其中某个量的值。
■解题思路:
熟练掌握总和与平均数之间的切换。
专题七 牛吃草问题
■核心公式:
草原原有草量=(牛数-每天长草量)×天数
■常见题型:
题目给出一块草地,××头牛吃××天,××头牛吃××天,则××头牛吃多少天?
■解题思路:
根据牛吃草问题的核心公式及题目给出的两个条件,列方程解方程即可。
专题八 盈亏问题
■核心公式:
份数=(盈+亏)÷两次每份数量的差
总数量=每份数量×份数+盈(或-亏)
■常见题型:
把一定的数量分成一定的份数,其中数量和份数都是未知的,题目给出的条件是任意两次试分后的每份数量及盈(或亏)数量,求总数量和份数。
■解题思路:
若题目待求量为总数量,则直接代入进行验证即可;若题目待求量为份数,则直接应用盈亏问题核心公式即可。
专题九 年龄问题
■核心知识:
任意两个人的年龄差始终保持不变。
两个人的年龄倍数随着时间的推移不断减小。
■解题思路:
1. 解题时,一定要抓住年龄差保持不变这个解题关键。
2. 直接代入法和列方程是常用方法。当题目所涉及的各人的年龄均在选项中时,可直接代入进行验证。当列方程时,多是根据年龄差保持不变建立等量关系。
专题十 时钟问题
■核心知识:
时针与分针一昼夜重合22次,垂直44次,成180°也是22次。
时钟一圈分成了12大格、60小格,时针每小时转1大格、5小格,分针每小时转12大格、60小格。分针与时针的速度比为12:1。
钟面问题很多本质上是追及问题,核心公式为 。其中 为真实追及时间,即分针和时针要达到条件要求的真实时间, 为静止时间,即假设时针不动,分针和时针达到条件要求的时间。
■常见题型:
1. 给定时间段,考查时针分针成某角度(如重合、成直角等)的次数。
2. 从某个时刻出发,考查多长时间后,时针、分针达到某要求。
■解题思路:
1. 对考查时针、分针成某角度的次数问题,重点考查时针、分针的运动轨迹即可得出答案。某些时候可通过对钟表进行实际操作得到答案。
2. 对考查达到条件要求所需时间的问题,先假设时针不动,将此时所需的时间代入核心公式即可。
数量智力测验题
可能很多考生会觉得,公务员考试的题目都应该是极其严肃的,但事实上并不尽然。在行政职业能力测验的数学运算部分,有一部分题目略显与众不同,带有比较强的智力性和趣味性。这些题目有个共同的特点,在计算上通常并不复杂,但往往要求考生有比较严密的思维和比较灵活的想法,与传统的数学题目相比,更多的带有一种“脑筋急转弯”的性质。而且对于某些题目,仅仅具备数学知识还不够,需要考生掌握一定的生活相关常识才能够求解。
一、抽屉原理类
“抽屉原理”也称“鸽巢原理”,最早由德国数学家狄利克雷提出,在组合数学中有非常重要的地位。如果用通俗一点的语言来描述,抽屉原理最常见的情形是:把多于n个的物体放到n个抽屉里,那么至少有一个抽屉里面要放有2个或2个以上的物体。在国家公务员考试中,抽屉原理类型的题目便曾经多次出现,其特征是,在题干中有“至少”和“保证”这两个词或类似的字样,比如:
2004年国家公务员考试B卷48题:有红、黄、蓝、白珠子各10粒,装在一只袋子里,为了保证摸出的珠子有两粒颜色相同,应至少摸出几粒( )A.3 B.4 C.5 D.6
【解析】:从“至少”和“保证”两个词我们可以判断,这是一道典型的抽屉原理问题。解决此类问题,有一个总体上的原则,就是始终考虑最坏的情况。对于本题,最坏的情况就是每种颜色的珠子恰好各摸出一粒,没有任何两粒的颜色相同。这时只要再摸出一粒,不管是何种颜色,都能保证有两粒颜色相同的珠子了。对于任何的抽屉原理问题,实际上都是遵循这样一个大的原则来求解。
2007年国家公务员考试49题:从一副完整的扑克牌中至少抽出( )张牌才能保证至少6张牌的花色相同.A.21B.22 C.23 D.24
【解析】:本题也可以很轻易的判断出属于抽屉原理类,依照“最坏的情况”来考虑,应该是每种花色的牌恰好都抽出了5张。这里涉及到生活中的小常识,首先考生要知道一副扑克牌中有四种花色的牌,第二这道题有一个小小的陷阱,那就是一副完整的扑克牌中还有两张大小王。所以如果考虑不够全面的话,本题很可能得到21张的答案,实际上真正最坏的情况就是连大小王也摸到了,需要摸23张才能保证有6张牌花色相同。
二、排列组合类
提到排列组合问题,有一部分考生可能要开始头疼了,因为这在公务员考试中是一个“超纲”知识点。在前面的系列文章中我们曾经提到过,绝大部分数学题目的基本解题知识点都囊括在初二数学大纲中,但排列组合是高中数学才接触到的内容。尽管如此,却并不意味着这一类型的题目很难,因为对于排列数和组合数的复杂计算性质,在解题中基本上是用不到的。对于绝大多数的排列组合题目,只要掌握了乘法原理和加法原理两种简单的方法就能够解决,稍复杂的题目需要用到最基本的组合数。首先来交代一下,什么叫做乘法原理和加法原理。
乘法原理,也叫分布计数原理,是指完成一件事需要分成n个步骤,做第一步有m1种不同的方法,做第二步有m2种不同的方法,……,做第n步有mn种不同的方法,那么完成这件事共有N=m1×m2×……×mn种不同的方法。
加法原理,也叫分类计数原理,是指完成一件事,有n类办法,在第一类办法中有m1种不同的方法,在第二类办法中有m2种不同的方法,……,在第n类办法中有mn种不同的方法,那么完成这件事共有N=m1+m2+……+mn种不同的方法。
在具体题目中,到底应该应用乘法原理还是加法原理,关键是看完成整个事件是否有步骤之分。必须按照步骤先后顺序进行的,应适用乘法原理;各办法之间互斥,不用分成步骤完成的,应适用加法原理。对于某些题目,还可能需要将两种原理组合应用。
2004年国家公务员考试B类44题把4个不同的球放入4个不同的盒子中,有多少种放法( )A.24 B.4C.12D.10
【解析】:因为球需要一个一个的放,只有将4个球全部放入盒子中才算完成,因此存在先后的步骤之分,应采用乘法原理。第一个球放到盒子中有4种不同的放法,第二个球只剩了3个盒子可以放,因而有3种放法,依此类推,放第三个球有2种放法,放第四个球只有1种放法,总的放法数目应该是各放法的乘积,即4×3×2×1=24种
2004年国家公务员考试A类47题林辉在自助餐店就餐,他准备挑选三种肉类中的一种肉类,四种蔬菜中的二种不同蔬菜,以及四种点心中的一种点心。若不考虑食物的挑选次序,则他可以有多少不同的选择方法( )A.4 B.24 C.72 D.144
【解析】:首先明确,三种食物要依次拿取,并且全部拿取之后才能算作挑选完毕,因此在肉类、蔬菜、点心三种食物之间应该应用乘法原理,以“×”连接。接下来考查每种食物的选择方法,在三种肉类中挑选一种只有3种方法,四种点心中挑一种也只有4种方法,本题的关键在于蔬菜。挑选第一种蔬菜可以有4种方法,再挑选第二种蔬菜有3种方法,但挑选蔬菜的方法却不是4×3=12种,因为题目中有一句话,“不考虑食物的挑选次序”。打个比方,先挑选土豆后挑选胡萝卜,与先挑选胡萝卜后挑选土豆,在本题中视作同一种选择方法,也就是说挑选蔬菜的方法只有6种。因此总的选择方法是4×3×6=72种。
2005年国家公务员考试一卷48题从1,2,3,4,5,6,7,8,9中任意选出三个数,使它们的和为偶数,则共有( )种不同的选法A.40B.41 C.44 D.46
【解析】:要使三个数的和为偶数,可以有两种情况,即三个数都是偶数或者一个是偶数两个是奇数,明显在这两种情况之间应该适用加法原理,接下来分别考查这两种情况。第一种情况,在四个偶数中选择三个,和在四个偶数中只选择一个的方法数其实是一致的,应该有4种。第二种情况,在四个偶数中选择一个有4种方法,在五个奇数中选择两个的方法数与例题4中类似,应该有(5×4)/2=10种,所以第二种情况共有4×10=40种方法。因此总的选择方法数应为4+40=44种。
2009年国家公务员考试115题要求厨师从12种主料中挑选出2种,从13种配料中挑选出3种来烹饪某道菜肴,烹饪的方式共有7种,那么该厨师最多可以做出多少道不一样的菜肴( )A.130468B.131204 C.132132 D.133456
【解析】:本题在本质上和例题4并无分别,只是从13种配料中挑选3种的方法需要用到基本的组合数。对于组合数的计算方法,有一个比较容易记忆的办法,即 ,分母分子各自为由m、n开始的m个数之乘积。根据这一公式,可以做出的总菜肴数应为 种。最后答案的求得,可以借助尾数原则,或者利用总方法数能被7整除的性质,直接锁定C选项。
三、“脑筋急转弯”
这里打了个引号,因为毕竟考试题目不等同于真正的脑筋急转弯,但其中的相似性非常大,不重于算而重在想。这类题目在公务员考试中尽管涉猎不多,但不失为一道独特的风景线。
2006年国家公务员考试二卷33题如果4个矿泉水空瓶可以换一瓶矿泉水,现有15个矿泉水空瓶,不交钱最多可以喝矿泉水( )A.3瓶 B.4瓶 C.5瓶 D.6瓶
【解析】:本题有一个争议点,就是能不能先借一个空瓶,然后再还回去。如果可以借1个空瓶,那就应该能喝到5瓶水,而如果不能借,便只能喝到4瓶。对于公务员考试的数学题,有一个大的原则,题目中给出的条件可以不用,但没有给出的条件不能乱用。本题中并没有给出“可以借瓶子”的条件,是不是就意味着就应该选择4瓶呢?这里要注意了,这类题目本身隐含了“可以借瓶子”的条件,因为在
2004年上海市公务员考试中曾经出现过类似题目:某品牌啤酒可以用3个空瓶再换回1瓶啤酒,某人买回10瓶啤酒,则他最多可以喝到( )瓶啤酒。A.13 B.15 C.16D.17
如果不能借一个空瓶,那么最多可以喝14瓶啤酒,此题没有正确答案。因此,在公务员考试中只要出现了空瓶换水这种类型的问题,都默认了一个“可以借瓶子”的条件。
2007年国家公务员考试54题32名学生需要到河对岸去野营,只有一条船,每次最多载4人(其中需1人划船)往返一次需5分钟。如果9时整开始渡河,9时17分时,至少有( )人还在等待渡河。 A.16 B.17 C.19 D.22
【解析】:本题实际上也有两个隐含的条件,第一,船必须由人划回来而不可能从河对岸“发气功”推回来;第二,每次只有1个人划船回来,而不可能4个人划过去3个人划回来。明确这两个条件后,可以轻易算出17分时已经有3×3=9个人在河对岸,而船上还有4个人,等待渡河的人数应为32—9—4=19人。
纵观历年来在公务员考试中出现过的智力型问题,在数学运算中占到的比重其实并不大,但这类题目贴近生活,对于解题需要的知识性或技巧性要求不高。而且由于这些题目的计算量都比较小,算数不复杂,因此也应该成为在考场上必须争取的对象之一。只要掌握了基本的解题方法和思考方向,再辅以适当的练习,对于这些智力测验性质的题目,相信考生们是有能力顺利拿下的。
 爱华网
爱华网