18 一月, 2013, oldlee11, R语言与数据挖掘, R语言同数据统计/分析, 因子分析, 聚类分析, , 0
函数库
?
001
002
003
004
005
006
007
008
009
010
011
012
013
014
015
016
017
018
019
020
021
022
023
024
025
026
027
028
029
030
031
032
033
034
035
036
037
038
039
040
041
042
043
044
045
046
047
048
049
050

051
052
053
054
055
056
057
058
059
060
061
062
063
064
065
066
067
068
069
070
071
072
073
074
075
076
077
078
079
080
081
082
083
084
085
086
087
088
089
090
091
092
093
094
095
096
097
098
099
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
#*************因子分析-R语言实现,函数库文件**************#
#****作者:oldlee11***************************************#
#****版本:v0.1*******************************************#
#****时间:2013-1-17*************************************#
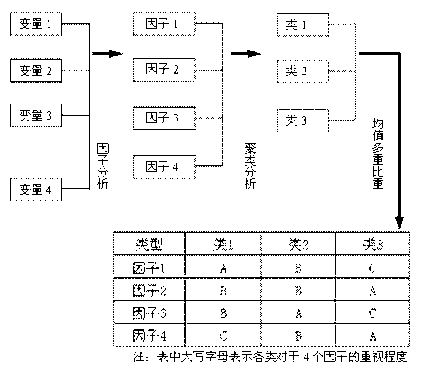
#功能目标:原始数据变量x1,x2,x3....xn(全体记为X)。通过样本可以知道某些变量之间有相关性。
# 则计算出新变量/因子f1,f2,f3....fm(m<n)(全体记为F),这新变量/因子F可以最大程度的表达原变量X
# 由于新变量的个数m小于原始变量个数n,即降维了。
#原理:AF+e=X
# A叫因子载荷(loading)。意义:fi(某1个因子)和xi(某一个原变量)的相关系数,接近1表示fi和xi相关性强:aij=cov(xi,fj)
# e叫特殊因子
#其它术语变量:
# 公因子方差:F(所有因子)解释xi(某一个原始变量)的方差百分比(贡献)
# 特征值:fi(某一个因子)解释X(所有原始变量)的方差百分比(贡献)
# 因子得分:在计算得出了A后,计算F内的样本数据。
# 旋转:对因子载荷进行旋转,之后因子载荷各项大的越来越大,小的越来越小,便于划分因子和原始变量的关系。
#****函数:factor()
#****概要:因子分析法
#****输入:
# 名称 | 数据格式
# data_frame | 欲分析的数据 ,数据框格式,最好带名称,不可以有factor分类数据
# factors | 欲产生的因子个数小于原始数据的变量个数
# scores | 是否进行因子得分
# rotation | 是否进行旋转
# loadings.abs.std | 用于从因子载荷中挑出那些原始变量和那些因子相关的标准(相对系数的绝对值的最低标准)
#****输出:
# factanal(..)产生的结果
# factanal(..)$score并非数据框格式,需要as.data.frame(factanal(..)$score)转化一下才是数据框格式。
factor<-function(data_frame,factors=2,scores="none",rotation="none",loadings.abs.std=0.6){
sol<-factanal(~.,data=data_frame,factors=factors,scores=scores,rotation=rotation)#使用最大似然法进行的因子分析。
print("==========================")
print("==== 因子分析结果如下 ====")
print("==========================")
print("模型:X=AF+e")
print("======================================================================")
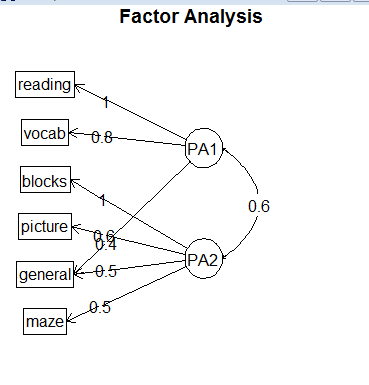
print("1 A即因子载荷loadings:")
print(" 每个数据(aij)表示了原始变量xi和因子变量fj的相关系数cov.值约接近+1或-1,约相关")
for(i in 1:factors){
print(paste(" 因子",i,"同原始变量的相关性系数"))
print(rev(sort(loadings(sol)[,i])))
}
#### 给出因子和原始变量的可能关系####
print(" 您可以通过以上数据查看接近+1或者-1的数据,以说明某一因子和那些原始变量相关,并分析该因子的隐含意义")
print(paste(" 依据相对系数的绝对值大于在",loadings.abs.std,"原则,我们建议如下:"))
tmp.x<-0#用于记录因子载荷大于loadings.abs.std的所有原始变量的序列号
dev.new()#新窗口# 画出每个因子对应各个变量的柱状图
par(mfrow=c(1,factors))#把窗口分为:1行3列
for(i in 1:factors){
tmp.x.factor<-0#用于记录某一因子中因子载荷大于loadings.abs.std的原始变量的序列号
print(paste(" 因子",i,"可以代表原始变量:"))
print.con<-""
for(j in 1:length(names(data_frame))){
if(abs(loadings(sol)[,i][j])>loadings.abs.std){#loadings.abs.std为相对系数的绝对值的最低标准
print(paste(" ",print.con,names(loadings(sol)[,i][j]),loadings(sol)[,i][j]))
tmp.x<-c(tmp.x,j)
tmp.x.factor<-c(tmp.x.factor,j)
}
}
data1<-sol$loadings[,i]
data1[-tmp.x.factor]<-0
data2<-sol$loadings[,i]
data2[tmp.x.factor]<-0
barplot(data1,horiz=TRUE,main=paste("因子",i,"的载荷"),col="red",xlim=c(-1,1))
barplot(data2,horiz=TRUE,add=TRUE)
}
tmp.x<-tmp.x[-1]
print(" 没有被代表的原始变量有:")
for(i in names(data_frame)[-as.numeric(names(table(tmp.x)))]){
print(paste(" ",i))
}
tmp.x.table<-table(tmp.x)
for(i in 1:length(tmp.x.table)){
if(tmp.x.table[i]>1){
print(paste(" Warings:原始变量",names(data_frame)[as.numeric(names(tmp.x.table[i]))],"被",tmp.x.table[i],"个因子共同代表了"))
}
}
print("2 特殊值:")
print("======================================================================")
ssloadings<-sol$loadings[1,]
for(i in 1:factors){
ssloadings[i]<-sum((sol$loadings[,i])^2)
}
var.sum<-length(names(data))#是每组xi数据标准化后(方差=1)的和=1*原始变量的个数
tmp<-0
tmp.vector<-sol$loadings[1,]#每个因子对应的累计贡献比例
for(i in 1:factors){
print(paste(" 因子",i,"可以解释所有原始变量X", round(10000*ssloadings[i]/var.sum)/100,"%的方差"))
tmp<-(ssloadings[i]/var.sum)+tmp
tmp.vector[i]<-tmp
print(paste(" 因子1至",i,"累计可以解释所有原始变量X", round(10000*tmp)/100,"%的方差"))
print("")
}
print(" 请查看所有因子的累计方差贡献比例,一般来说要大于80%,否则说明因子数目不足")
dev.new()#新窗口#画出累计方差贡献比例
#barplot(tmp.vector,ylim=c(0,1),main="各个因子对整体方差的累计贡献率ssloadings(特征值)")
barplot(ssloadings/var.sum,ylim=c(0,1),main="各个因子对整体方差的贡献率")
lines(tmp.vector,col="blue",lwd=2)
points(c(1:factors),tmp.vector)
text(c(1:factors),tmp.vector+0.05,labels=round(tmp.vector*10000)/10000)
abline(h=0.8,col="red")
print("======================================================================")
print("3 因子得分:")
print(" 使用新产生的因子来表示原来的样本")
print(" 注意:每组因子对应的样本数据(即:每一列)已经经过了标准化:均值约为0,标准差约为1")
print(sol$score)
sol
}
##############系统聚类法:对新样本进行距离############################################
hc<-function(data_frame,k.num){
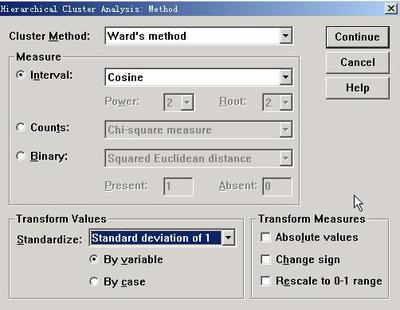
d<-dist(scale(data_frame))#scale是标准化公式
hc<-hclust(d)
dev.new()
plclust(hc,hang=-1)
re<-rect.hclust(hc,k=k.num,border="red")#划分5个聚类,re[[i]]是第i个聚类包含的样本id向量。
dev.new()
hc.point<-data_frame[1:k.num,]#用于存储每个聚类里个变量的平均值
for(i in 1:k.num){
for(j in 1:length(names(data_frame))){
hc.point[i,j]<-mean(data_frame[re[[i]],j])
}
}
#stars(hc.point+1+round(abs(min(hc.point))))#由于hc.point被标准化,所有有负数,无法使用星图表示,现全体加一个数字,使不再有负数。
#dev.new()
stars(hc.point+1+round(abs(min(hc.point))),full=F,draw.segments=T,key.loc=c(5,0.5),mar=c(2,0,0,0))
dev.new()
stars(hc.point,full=F,draw.segments=T,key.loc=c(5,0.5),mar=c(2,0,0,0),main="不平移")#不知到底使用要平移
hc.point
}
测试程序:
#test1#48个应聘者的15个指标的得分和id号,得分为0-10
data<-read.csv("d://r//factor//applicant.csv")
data<-data[-1]
sol.factor<-factor(data,factors=5,scores="Bartlett",rotation="varimax");
结果:
[1] "=========================="
[1] "==== 因子分析结果如下 ===="
[1] "=========================="
[1] "模型:X=AF+e"
[1] "======================================================================"
[1] "1 A即因子载荷loadings:"
[1] " 每个数据(aij)表示了原始变量xi和因子变量fj的相关系数cov.值约接近+1或-1,约相关"
[1] " 因子 1 同原始变量的相关性系数"
SC AMB SMS LC GSP DRV POT
0.91661844 0.90887444 0.88014177 0.85117729 0.78335594 0.75419498 0.71687415
APP KJ SUIT HON LA FL EXP
0.45087828 0.41774040 0.35058165 0.22821711 0.22162986 0.12746670 0.08041938
AA
0.05933985
[1] " 因子 2 同原始变量的相关性系数"
EXP SUIT FL KJ DRV POT
0.77266335 0.76449559 0.72162726 0.39865243 0.39271661 0.36249122
GSP SMS LA AMB APP AA
0.29450872 0.26601944 0.24577719 0.18712315 0.13392291 0.12887303
LC SC HON
0.12471808 -0.09322833 -0.21981125
[1] " 因子 3 同原始变量的相关性系数"
LA HON KJ POT GSP
0.827370568 0.776987127 0.562811285 0.445529774 0.354466962
LC APP DRV SC AMB
0.278766832 0.269544890 0.198824418 0.166868929 0.112465561
SMS FL SUIT AA EXP
0.111066506 0.101977041 0.058179578 0.002176755 -0.049844918
[1] " 因子 4 同原始变量的相关性系数"
AA POT APP EXP GSP
0.6863156611 0.2672573067 0.2056070064 0.1705401447 0.1480620949
SUIT LC HON AMB DRV
0.1478674226 0.0249597130 -0.0004074814 -0.0365023678 -0.0395939658
SMS LA SC FL KJ
-0.0473907568 -0.0561707141 -0.0720675452 -0.1173475356 -0.5851358195
[1] " 因子 5 同原始变量的相关性系数"
APP AMB DRV HON KJ
0.258158383 0.165496223 0.113689366 0.063946654 0.049305338
POT EXP AA SC SUIT
0.020647994 0.018167169 0.016387719 0.015079928 -0.005404459
FL SMS LA GSP LC
-0.009679265 -0.012552488 -0.078570813 -0.181440791 -0.420287717
[1] " 您可以通过以上数据查看接近+1或者-1的数据,以说明某一因子和那些原始变量相关,并分析该因子的隐含意义"
[1] " 依据相对系数的绝对值大于在 0.6 原则,我们建议如下:"
[1] " 因子 1 可以代表原始变量:"
[1] " SC 0.916618443168082"
[1] " LC 0.851177293416533"
[1] " SMS 0.880141769968176"
[1] " DRV 0.754194978394463"
[1] " AMB 0.908874438992514"
[1] " GSP 0.783355944976582"
[1] " POT 0.716874152279818"
[1] " 因子 2 可以代表原始变量:"
[1] " FL 0.721627255740438"
[1] " EXP 0.77266334848744"
[1] " SUIT 0.764495589647711"
[1] " 因子 3 可以代表原始变量:"
[1] " LA 0.827370568125198"
[1] " HON 0.776987126787634"
[1] " 因子 4 可以代表原始变量:"
[1] " AA 0.686315661069076"
[1] " 因子 5 可以代表原始变量:"
[1] " 没有被代表的原始变量有:"
[1] " APP"
[1] " KJ"
[1] "2 特殊值:"
[1] "======================================================================"
[1] " 因子 1 可以解释所有原始变量X 36.6 %的方差"
[1] " 因子1至 1 累计可以解释所有原始变量X 36.6 %的方差"
[1] ""
[1] " 因子 2 可以解释所有原始变量X 16.71 %的方差"
[1] " 因子1至 2 累计可以解释所有原始变量X 53.31 %的方差"
[1] ""
[1] " 因子 3 可以解释所有原始变量X 14.59 %的方差"
[1] " 因子1至 3 累计可以解释所有原始变量X 67.9 %的方差"
[1] ""
[1] " 因子 4 可以解释所有原始变量X 6.85 %的方差"
[1] " 因子1至 4 累计可以解释所有原始变量X 74.75 %的方差"
[1] ""
[1] " 因子 5 可以解释所有原始变量X 2.2 %的方差"
[1] " 因子1至 5 累计可以解释所有原始变量X 76.96 %的方差"
[1] ""
[1] " 请查看所有因子的累计方差贡献比例,一般来说要大于80%,否则说明因子数目不足"
[1] "======================================================================"
[1] "3 因子得分:"
[1] " 使用新产生的因子来表示原来的样本"
[1] " 注意:每组因子对应的样本数据(即:每一列)已经经过了标准化:均值约为0,标准差约为1"
data<-as.data.frame(sol.factor$score)
sol.hc<-hc(data,k.num=4)
结果:
补充数据applicant.csv
X FL APP AA LA SC LC HON SMS EXP DRV AMB GSP POT KJ SUIT
1 1 6 7 2 5 8 7 8 8 3 8 9 7 5 7 10
2 2 9 10 5 8 10 9 9 10 5 9 9 8 8 8 10
3 3 7 8 3 6 9 8 9 7 4 9 9 8 6 8 10
4 4 5 6 8 5 6 5 9 2 8 4 5 8 7 6 5
5 5 6 8 8 8 4 4 9 5 8 5 5 8 8 7 7
6 6 7 7 7 6 8 7 10 5 9 6 5 8 6 6 6
7 7 9 9 8 8 8 8 8 8 10 8 10 8 9 8 10
8 8 9 9 9 8 9 9 8 8 10 9 10 9 9 9 10
9 9 9 9 7 8 8 8 8 5 9 8 9 8 8 8 10
10 10 4 7 10 2 10 10 7 10 3 10 10 10 9 3 10
11 11 4 7 10 0 10 8 3 9 5 9 10 8 10 2 5
12 12 4 7 10 4 10 10 7 8 2 8 8 10 10 3 7
13 13 6 9 8 10 5 4 9 4 4 4 5 4 7 6 8
14 14 8 9 8 9 6 3 8 2 5 2 6 6 7 5 6
15 15 4 8 8 7 5 4 10 2 7 5 3 6 6 4 6
16 16 6 9 6 7 8 9 8 9 8 8 7 6 8 6 10
17 17 8 7 7 7 9 5 8 6 6 7 8 6 6 7 8
18 18 6 8 8 4 8 8 6 4 3 3 6 7 2 6 4
19 19 6 7 8 4 7 8 5 4 4 2 6 8 3 5 4
20 20 4 8 7 8 8 9 10 5 2 6 7 9 8 8 9
21 21 3 8 6 8 8 8 10 5 3 6 7 8 8 5 8
22 22 9 8 7 8 9 10 10 10 3 10 8 10 8 10 8
23 23 7 10 7 9 9 9 10 10 3 9 9 10 9 10 8
24 24 9 8 7 10 8 10 10 10 2 9 7 9 9 10 8
25 25 6 9 7 7 4 5 9 3 2 4 4 4 4 5 4
26 26 7 8 7 8 5 4 8 2 3 4 5 6 5 5 6
27 27 2 10 7 9 8 9 10 5 3 5 6 7 6 4 5
28 28 6 3 5 3 5 3 5 0 0 3 3 0 0 5 0
29 29 4 3 4 3 3 0 0 0 0 4 4 0 0 5 0
30 30 4 6 5 6 9 4 10 3 1 3 3 2 2 7 3
31 31 5 5 4 7 8 4 10 3 2 5 5 3 4 8 3
32 32 3 3 5 7 7 9 10 3 2 5 3 7 5 5 2
33 33 2 3 5 7 7 9 10 3 2 2 3 6 4 5 2
34 34 3 4 6 4 3 3 8 1 1 3 3 3 2 5 2
35 35 6 7 4 3 3 0 9 0 1 0 2 3 1 5 3
36 36 9 8 5 5 6 6 8 2 2 2 4 5 6 6 3
37 37 4 9 6 4 10 8 8 9 1 3 9 7 5 3 2
38 38 4 9 6 6 9 9 7 9 1 2 10 8 5 5 2
39 39 10 6 9 10 9 10 10 10 10 10 8 10 10 10 10
40 40 10 6 9 10 9 10 10 10 10 10 10 10 10 10 10
41 41 10 7 8 0 2 1 2 0 10 2 0 3 0 0 10
42 42 10 3 8 0 1 1 0 0 10 0 0 0 0 0 10
43 43 3 4 9 8 2 4 5 3 6 2 1 3 3 3 8
44 44 7 7 7 6 9 8 8 6 8 8 10 8 8 6 5
45 45 9 6 10 9 7 7 10 2 1 5 5 7 8 4 5
46 46 9 8 10 10 7 9 10 3 1 5 7 9 9 4 4
47 47 0 7 10 3 5 0 10 0 0 2 2 0 0 0 0
48 48 0 6 10 1 5 0 10 0 0 2 2 0 0 0 0
 爱华网
爱华网