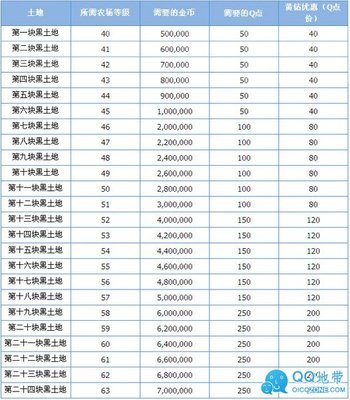
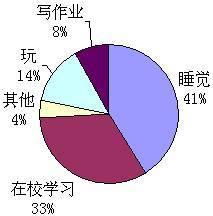
转引自http://chinadoctor.org/doctor/news/technology/1504.htm
置信区间或称置信间距,是指在某一置信度时,总体参数所在的区域距离或区域长度。
置信度又称显著性水平,意义阶段,信任系数等,是指估计总体参数落在某一区间时,可能犯错误的概率,用符号α表示。
例如.95置信区间是指总体参数落在该区间之内,估计正确的概率为95%,而出现错误的概率为5%(α=.05),由此可见:
.95置信间距=.05显著性水平的置信间距,或.05置信度的置信间距。
.99置信间距=.01显著性水平的置信间距,或.01置信度的置信间距。
显著性水平在假设检验中,还指拒绝虚无假设时可能出现的犯错误的概率水平。
区间估计的原理与标准误
区间估计是根据样本分布的理论,用样本分布的标准误(SE)计算区间长度,解释总体参数落入某置信区间可能的概率。
区间估计包括成功估计的概率大小及估计范围大小两个问题。人们在解决实际问题时,总希望估计值的范围小一点,成功的概率大一些。但在样本容量一定的情况下,二者不可兼得。如果使估计正确的概率加大些,势必要将置信区间加长,若使正确估计的概率为1.00,即完全估计正确,则置信区间就会很长,也就等于没作估计了。这就像在百分制的测验中你估计一个人的得分可能为0至100分之间一样。反之,如果要使估计的区间变小,那就势必会使正确估计的概率降低。
统计分析中一般规定:正确估计的概率,也即置信水平为.95或.99,那么显著性水平则为.05或.01,这是依据.05或.01属于小概率事件,而小概率事件在一次抽样中是不可能出现的原理规定的。
区间估计的原理是样本分布理论。即在进行区间估计值的计算及估计正确概率的解释上,是依据该样本统计量时分布规律样本分布的标准误(SE)。也就是说,只有知道了样本统计量的分布规律和样本统计量分布的标准误才能计算总体参数可能落入的区间长度,才能对区间估计的概率进行解释,可见标准误及样本分布对于总体参数的区间估计是十分重要的。样本分布可提供概率解释,而标准误的大小决定区间估计的长度,如果标准误越小可使置信区间的长度变短,而估计成功的概率仍可保持较高水平。一般情况下,加大样本容量可使标准误变小。
平均数分布的概率
下面以平均数的区间估计为例,说明如何根据平均数的样本分布及平均数分布的标准误,计算置信区间和解释成功估计的概率。第五章已讲到,当总体方差已知时样本平均数的分布为正态分布或渐近正态分布。
样本平均数的平均数?,平均数的离散程度即平均数分布的标准差(简称标准误写作?或?),
根据正态分布,可以说:
有68.26%的平均数落在μ±1标准误之间,
有95%的平均数落在μ±1.96标准误之间,
有99%的平均数落在μ±2.58标准误之间等等。
图6—1平均数分布的概率
或者说:
μ±1标准误之间包含所有平均数的68.26%,
μ±1.96标准误之间包含所有平均数的95%,
μ±2.58标准误之间包含所有平均数的99%,等等。
只要符合正态分布,平均数的分布一定遵循按正态分布理论所计算出的概率。
平均数的区间估计
可是在实际的研究中,只能得到一个样本的平均数,我们可将这个样本平均数看作无限多个样本平均数之中的一个。当只知样本平均数(),而不知总体平均数时,可根据平均数的样本分布进行推理。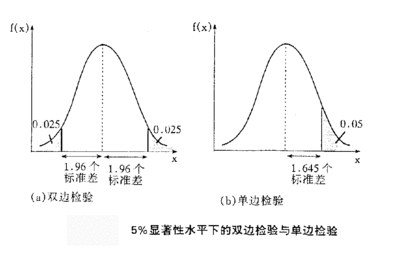
如果有所有平均数的68.26%的平均数落在μ上下一个标准误之间,那么可以推理:所有平均数中有68.26%的平均数加上一个或减去一个标准误这一间距之内将包含总体参数μ,也就是说有68.26%的机会被包含在任何一个平均数±1标准误之间,或者说,估计μ在平均数±1标准误之间正确的概率为68.26%。同样的道理可以说:μ在平均数±1.96标准误之间的正确概率为95%,μ在平均数±2.58标准误之间的正确概率为99%,以及其他任何可能的概率。那为什么置信区间用平均数加、减一定数量的标准误来计算呢?这是因为样本平均数究竟μ落在的左侧还是右侧是不知道的,故用平均数±Zα/2标准误(Zα/2为样本分布的横坐标值),这一段距离表示置信区间。如果能知平均数落在μ的左侧,那么平均数至平均数+1.96标准误这一区间内包含μ的可能为97.5%,若能确知平均数在μ之右侧,那么平均数至平均数+1.96标准误这一区间包含μ的可能亦为97.5%,这样不仅可以缩短置信区间的长度,还可提高正确估计的概率,但事实上这是做不到的。见图6—2
图6-2 平均数的区间估计
置信度
当推论出总体参数μ按一定的概率落在某一置信区间时,实际的均值究竟落在分布的哪个位置上并不能确知,它也有可能落在分布的两侧尾部,这时若说μ在平均值±Zα/2标准误之间便是错误的了,不过出现这种错误的可能概率可以根据样本分布进行计算:其概率为α。例如估计μ在平均数±1.96标准误之间正确的概率为95%,则错误的概率为5%,这5%来自样本分布的左右两尾端各2.5%的样本平均数,因为这些平均数±1.96标准误这一段距离中并不包含μ在内。见图6-3:
图6-3置信度示意图
其他总体参数的估计原理与平均数的估计原理相同,但所依据的样本分布及标准误不同。
本文来源于 响石潭 http://www.chinadoctor.org
另请参阅:置信区间
 爱华网
爱华网