《正弦函数、余弦函数的图象》教学案例
数学科组金莹
【案例背景】
在接到“青年教师教学优质课比赛”的任务没多久,我又被级组赋予另一项艰巨而伟大的使命“优质班会课评比”。当两个“优质课”碰撞时,也许就只能成全一个“优质”了!刚从班会优质课的赛场退下来,还没来得及喘口气,便又匆忙的投入几天后即将举行的教学优质课。虽然我早已不是一位新手,我的年龄也正在踩线,青年教师的青春头衔将不再属于我,可是,面对教研处浓重组织的这场教学比赛,我还是心惊胆战!一是对手实在太强大;二是已有好几年没有教高一;三是《三角函数》是个公认不好讲、不易出彩的内容;四是我的准备不充足,留给我的时间太少了。面对这么多的不利因素,我只能勇往直前,不怕失败!首先,确定主题。怎样跳出三角函数那些枯燥的公式,平淡的性质,以学生为主体,新授课上出探究味呢?经过思考、对比,唯有“图象”,能当此重任。它有“形”的直观,有多媒体的动态,更有学生参与画图的空间。于是,我将主题定为“正弦函数、余弦函数的图象”。这是一个承前启后的章节,它的推导要利用前面讲过的三角函数线,它的出现又将为后面研究性质铺路。这也是一个知识联系丰富的内容,从正弦到余弦,只需用诱导公式和图象变换可以实现;从三角函数线几何法作图,到简化的五点法作图,再到灵活的图象变换,方法多样,内涵丰富。另外,这节课的画图,需要强大的信息技术支持,课件的动画效果和设计,直接影响到本课的难点突破。在这方面,我也花了大量心血,最终的课件效果令人满意,被其他老师借用。分享是一种快乐和美德!
【案例描述】
本节课需要用到很多以前的知识,比如,一开始给出正弦函数的定义,这需要以函数的定义为基础。而函数概念放了很久,学生普遍会遗忘。再如,由正弦曲线图象得出余弦曲线的图象,要借助诱导公式五、六。画正弦曲线的几何方法,要利用正弦线。所以,在课前的学案中,我设计了【温故知新】环节,帮助学生回顾。本课还有一个难点,画正弦曲线时怎样引导学生联想到三角函数线中的正弦线?从而用几何法准确作图。为此,我又设计了一个铺垫。用问题串来引导,启发学生如何准确的画出纵坐标,从一个具体的点入手,从而有效突破难点。
部分课堂实录:
一.课题导入
师:同学们,通过前面的学习,我们知道,当角的概念推广之后,在弧度制下,实数集与角的集合之间就形成了一一对应的关系,而当角确定之后,正弦值随之确定,余弦值也随之确定,这样,任意给定的一个实数x,有唯一确定的值sinx(或cosx)与之对应。由这个法则所确定的函数y=sinx(或y=cosx)叫做正弦函数(或余弦函数).
师:正弦函数和余弦函数的定义域是多少?
生:定义域为R.
师:在遇到一类新的函数时,我们通常会先作出它的图象,然后通过图像来研究它的性质.
通过图象可以研究函数的哪些性质?
生:值域、单调性、奇偶性、最大值、最小值等.
师:这节课我们首先来研究正弦函数和余弦函数的图象.
(教师板书,引出课题:正弦函数、余弦函数的图象)
师:在研究正弦函数和余弦函数图象之前,请同学们观看一个物理实验.
(多媒体展示“简谐运动的位移和时间关系”图象,让学生经历从“生活世界”到“科学世界”,感受三角函数变化的特定规律,并从直观上认识正弦函数和余弦函数图象.)
二.讲授新课
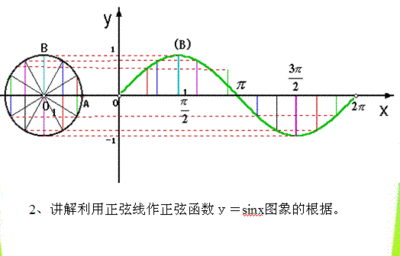
1.利用单位圆中的正弦线作函数y=sinx,x∈[0,2π]的图象
师:以前我们用描点法作函数图象的时候,一般分哪几个步骤?
生:列表、描点、连线.
师:在[0,2p]范围内取哪些点?
生:取特殊角:等。
师:那么的值是精确值还是近似值?
师生共同讨论总结描点法的弊端,当x取值时,y的值大都是近似值,加之作图上的误差,不易描出对应点的精确位置.
师:(进一步提出问题)为了得到比较精确的正弦函数的图象,如何从几何的角度用图形表示纵坐标?
比如,怎样用几何法描出点?
(教师引导学生进行分析:要作出比较精确的正弦函数的图象,关键是要把“列表”中的点的纵坐标精确的标出来,注意到点的纵坐标其实都是正弦值,因此,问题转化成如何在坐标系中表示正弦值。结合在前面已经学过的三角函数线——三角函数线从“形”的角度刻画了三角函数值的大小,这样学生很自然的想到利用单位圆中的正弦线来表示点的的纵坐标——正弦值.)
生:学生先探索,然后上黑板展示她的成果。
(这样设计比较自然,合理,符合学生认知的基本规律.)
师:既然我们能够利用正弦线准确描点,那么请同学们再多找一些点,画出正弦函数y=sinx,x?[0,2p]的图象。
(留时间给学生作图,教师巡视,学生画好后投影展示,并请学生讲解作图步骤。)
师:在学生讲解完后,教师再利用多媒体的动画效果演示一下作图过程,加深印象。
(对作图过程进行小结,让学生进一步体会用正弦线描点的精确性)
师:我们知道正弦函数的定义域是R,但是刚才得到的仅仅是[0,2π]上的图象.
提出问题:如何由y=sinx,x?[0,2p]的图象得到y=sinx,x?R的图象.
2.由函数y=sinx,x∈[0,2π]的图象得到函数y=sinx,x∈R的图象
教师结合图形,引导学生继续研究[2π,4π]上的图象,让学生观察,发现:[2π,4π]上的图象和[0,2π]上的图象都是由相同的正弦线通过平移过去得到的,因此,[2π,4π]上的图象和[0,2π]上的图象在形状上是完全一样的,只是位置不同,即要得到[2π,4π]上的图象只需把[0,2π]上的图象像右平移2π个单位,其他区间上的图象也可以用类似的方法得到.
师生形成共识:把函数y=sinx,x∈[0,2π]的图象沿x轴左右平移,每次平移2π个单位,就可以得到y=sinx,x∈R的图象.
师:多媒体演示由y=sinx,x∈[0,2π]的图象得到y=sinx,x∈R的图象的过程.
师:(小结)由y=sinx,x∈[0,2π]的图象得到y=sinx,x∈R的图象的过程中,我们实际上根据的是诱导公式一:sin(x+2kp)=sinx,k?Z.
(先让学生从直观上感受[2π,4π]上的图象,再用诱导公式一从理论的高度上解释、认识,学生较容易接受,如果一下就利用诱导公式一来解释由y=sinx,x∈[0,2π]的图象得到y=sinx,x∈R的图象的过程,比较抽象,学生不易理解)
- 由正弦函数的图象得到余弦函数的图象
师:(过渡)到这里,我们这节课的第一个问题——正弦函数的图象就解决了,对于余弦函数的图象,我们是否可以用类似的方法来研究?
生:可以,但比较麻烦.
师:想走捷径,就得利用前人的成果!能否以正弦函数的图象为基础,结合诱导公式快速作出余弦函数的图象?
探究:你能根据诱导公式,以正弦函数的图象为基础,通过适当的图象变换得到余弦函数的图象吗?
(教师组织学生讨论、交流引导学生利用诱导公式由正弦函数的图象得出余弦函数的图象,并动态演示过程.)
师:我们学过的哪个诱导公式能够实现正弦和余弦的互化?是需要把正弦化余弦,还是余弦化正弦?
生1:把余弦化正弦,;
师:(继续引导)还有没有其它的诱导公式能够实现余弦化正弦?
生2:;
师:(对学生的回答表示肯定与赞赏)非常好!要作的图象,只要作或的图象。从函数图象变换的角度考虑,如何由y=sinx的图象得到或的图象,哪一个更简单?
生:由y=sinx的图象得到的图象,需要经过两次图象变换,而由y=sinx的图象得到的图象只要经过一次变换即向左平移个单位,所以后者更简单.
师:这样,我们通过平移,就得到了余弦函数的图象.
(通过探究,使学生从函数解析式之间的关系思考函数图象之间的关系,进而学习通过图象变换画余弦函数图象的方法,向学生渗透化归转化的数学思想).
4.用“五点法”作正弦函数的简图
师:我们在作正弦函数y=sinx,x∈[0,2π]的图象时,描出了12个点,但其中起关键作用的点是哪些?分别说出它们的坐标。
(学生回答,教师动画演示)
师:在精确度要求不高的情况下,我们常用“五点画图法”作出正弦函数的简图。
师:你们能类比说出余弦函数的五个关键点吗?
(师生一起总结:“五点作图法”是我们画三角函数简图的基本方法。
师:(小结)到这里,我们这节课的两个问题就都解决了.我们主要是学习了作三角函数图象的两种方法:利用三角函数线作正弦函数的图象和利用“五点法”作正弦函数、余弦函数的简图.用三角函数线作函数的图象虽然精确但比较麻烦,在今后的学习中,我们更多的是用“五点法”,它更实用.
下面我们就一起用“五点法”来作与正弦函数和余弦函数有关的简单函数的图象.
三.典例讲解
示例1:(1)用“五点法”作函数y=1+sinx,x∈[0,2π]上的简图;
(2)用“五点法”作函数y=-cosx,x∈[0,2π]上的简图.
(对于(1),教师重点、详细讲解,并多媒体演示过程,对于(2),则由学生练习,独立完成.)
师:(进一步提出思考,引导学生从图象变换的角度了解图象间的关系)你能否从函数图象变换的角度出发,利用y=sinx,x?[0,2p]的图象,得到y=1+sinx,x?[0,2p]的图象?同样的,如何利用y=cosx,x?[0,2p]的图象,得到y=-cosx,x?[0,2p]的图象?
2、巩固练习
四、课堂小结
师:这节课的研究学习就到这里了,请大家回顾一下这节课的探索和收获.
生1:我们学习了用三角函数线作图,“五点法”作图;
生2:复习了诱导公式,并利用诱导公式从正弦函数图象变换得到余弦函数的图象。
师:(在学生自行总结的基础上补充总结)说的好!这些正是这节课的重点所在.
五、拓展提升
(留给学生课外思考,训练数形结合的思想方法。)
【案例评析】
比较成功的地方:
1.教学思路清晰,各个环节过渡比较自然,课堂教学设计得比较紧凑.
2.对于正弦曲线、余弦曲线首先从实验入手形成直观印象,然后探究画法,用最基本的“描点法”作图:列表,描点、连线。
3、有效的突破难点。本课的重心和难点几乎都压在前半段了,怎样启发学生联想到前面已经学过的三角函数线作图?这需要精心设问,悉心引导,才能成功搭桥。我从y的近似值开始质疑,先抛出一个具体的点,怎样用几何的方法画出呢?抓住了几何特征,学生就会慢慢想到正弦线。有了这个点的铺垫,后面的作图就不难,放手给学生画图。这样设计比较自然,合理,符合学生认知规律.
4、课件制作精美,动画效果好,能有力的辅助教学,给学生生动直观的印象。
5、体现了“以学生为主体,自主探究、合作交流”的新课标理念。从探究正弦函数的图象,到如何由正弦曲线得到余弦曲线,我都是给了充分的时间让学生去思考、交流、画图,还请了学生到黑板讲解。教师只是一个组织者。
6、精选习题,以点带面,层层递进。注意规范性和数学思想的渗透。
不足之处:
1、过于依赖多媒体演示,导致忽略了传统的、基本的板书设计。
2、由于本节课容量很大,新授课要讲清概念、原理、联系,往往需要花费较长的时间。再加上学生画图、探究,也需预留充分的时间给他们,导致在习题巩固环节很赶,有种前松后紧的感觉。
3、数学课要想上出数学味、趣味性,这跟内容有极大的关联。那些有思维深度的内容,如:解几、函数、数列,发挥探索的余地较大。概率统计等内容趣味性强,而中规中矩的三角函数,只能平平淡淡才是真!相对理科的物理、化学、生物,它们更贴近生活、应用,更容易吸引评为们的眼球。
4、由于教学优质课与班会优质课档期相撞,导致一心不能两用,准备不是很充分。
 爱华网
爱华网