从古至今,勾股定理的证明方法不下数百种。其中,下面这种证明方法,可算是最简单的了。
(1)取任意一个直角边为a、b,斜边为c的直角三角形;
(2)再取一个同样的直角三角形,放在它的右边,使两条直角边a、b连成一条直线;
(3)连接两个锐角的顶点,又得到一个两条直角边都是c的直角三角形。这3个直角三角形拼成了一个上底是a、下底是b、高是(a+b)的梯形(如图):
按照梯形面积公式,这个梯形的面积等于:
(a+b)(a+b)÷2
按照三角形面积公式,这个梯形的面积等于:
ab÷2+ab÷2+c2÷2
于是,
(a+b)(a+b)÷2=ab÷2+ab÷2+c2÷2
即,
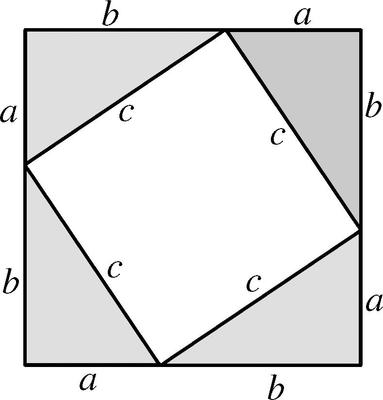
(a+b)(a+b)=ab+ab+c2
a2+2ab+b2=2ab+c2
a2+b2=c2
证明完毕。
是不是再简单不过了?!
勾股定理的这个证明,是美国第十七任总统加菲尔德给出的。连政治精英也如此钟情于数学,看来,数学的魅力真是无处不在!
 爱华网
爱华网