http://blog.csdn.net/sunfoot001/archive/2010/09/22/5900917.aspx
fft谱分析中的栅栏效应和频谱泄露
栅栏效应:
对采样信号的频谱,为提高计算效率,通常采用FFT算法进行计算,设数据点数为:
N = T/dt = T.fs
则计算得到的离散频率点为:
Xs(fi) , fi = i.fs/N , i = 0,1,2,.....,N/2
这就相当于透过栅栏观赏风景,只能看到频谱的一部分,而其它频率点看不见,因此很可能使一部分有用的频率成份被漏掉,此种现象被称为栅栏效应。
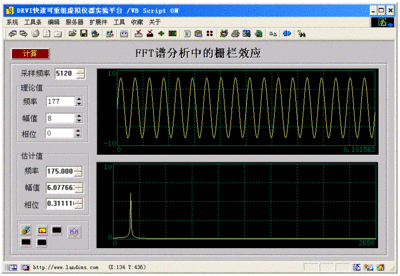
比如,通过以下的实验可以看到栅栏效应:
实验内容为用505Hz正弦波信号的频谱分析来说明栅栏效应所造成的频谱计算误差。
设定采样频率:fs=5120Hz,软件中默认的FFT计算点数为 512,其离散频率点为:
fi = i.fs/N = i.5120/512=10 , i= 0,1,2,....,N/2
位于505Hz 位置的真实谱峰被挡住看不见,看见的只是它们在相邻频率500Hz或510Hz处能量泄漏的值。
若设 fs=2560Hz,则频率间隔df=fs/N=5Hz,重复上述分析步骤,这时在505位置有谱线,我们就能得到它们的精确值。
从时域看,这个条件相当于对信号进行整周期采样,实际中常用此方法来提高周期信号的频谱分析精度。
频谱泄露:
工程实际中能观测到的信号不可能是无限长的,只能从某时刻开始观测有限时间长度T的一段,这就相当于用一个窗函数对信号进行截断:
xs(t)=x(t).u(t)
截断后信号的频谱为:
Xs(f)=X(f)*U(f)
若x(t)为一单一成份的正弦函数,u(t)为矩形窗函数
clc;
fs=1024;%采样频率为1000Hz;
N=2048;
t=0:1/fs:N/fs;%
x=3*cos(2*pi*56*t)+2*cos(2*pi*23*t);%产生正弦波信号;
subplot(2,1,1)
%plot(t(1:50),x(1:50));%画出时域内的信号前50个采样点;
plot(t(1:256),x(1:256));
Y=fft(x,N); %对X进行512点的傅立叶变换;
Y1=abs(Y);
Y2=Y1/(N/2);%换算成实际的幅度
f= (0:N)*fs/N; %设置频率轴(横轴)坐标,1000为采样频率;fs/N是每个采%样点对应的频率,*(0:N)为了让频率从0开始表示。
subplot(2,1,2)
plot(f(1:N/2),Y2(1:N/2));%画出频域内的信号
%%%%%%%%%%%%%%%%%wln%%%%%%%%%%%%%%%%%%%%%%%%
频率分辨率------------可以分辨出的频率最小间隔
对于t=0:1/fs:N/fs;其实写成t=0:1/fs:t0;t0>=N/fs好理解,这只是时间上的设置,与频谱泄露无关,只要t0>=N/f就行;但我们主要是为了求FFT的,故时间上写成t=0:1/fs:N/fs
采样频率确定为fs,原信号频率为f0,fs>=2f0,信号的分辨率比如对于x=3*cos(2*pi*504*t)+2*cos(2*pi*203.5*t);只有频率分辨率达到0.5,才能尽量减少频谱泄露。
采样频率fs=1024,采样点数为N=2048,则某点n所表示的频率为:Fn=(n-1)*fs/N,Fn所能分辨到频率为为fs/N=0.5。可以。
%%%%%%%%%%%%%%%%%wln%%%%%%%%%%%%%%%%%%%%%%%%
本文来自CSDN博客,转载请标明出处:http://blog.csdn.net/sunfoot001/archive/2010/09/22/5900917.aspx
 爱华网
爱华网