今天我要讲的是博弈论(也叫对策论),这本来是一门很深的学问,在学校里至少要讲一个学期,甚至还有专门的博士课程。但在这里我不可能讲这么多,我只能做一个简单的概括,把它的基本概念、研究方法和一般规律给大家介绍出来。
从囚犯难题说起
我们先从一个常见的案例说起。这个故事是这样的:
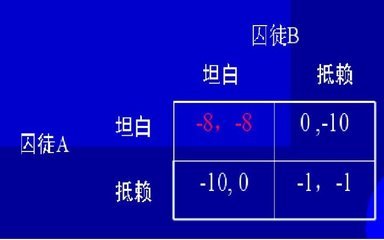
有一个富人在家中被谋杀,他的财产被盗。警方在侦讯过程中抓到两名嫌疑犯:甲和乙,并在他们家中搜出了被盗的财物。但甲、乙都否认杀人,声称他们进入被害 人家中时那个人已经死去。所以警方肯定他们至少犯下了盗窃罪,但对他们是否杀死了被害人并没有把握。于是警方在把他们隔离的情况下分别对他们表示:因为偷 东西已经有确凿证据,这将被判刑2年;如果拒不承认杀人而被另一方检举,将被判刑20年,而检举的一方可以受奖无罪释放;如果双方都坦白杀人,将各被判刑 10年。这样,甲乙可能面临的判决如下:
通过分析可以看出,最后的结果是甲乙都会承认杀人。因为对本人来说,不管对方承认不承认,自己承认总比不承认好。如果对方不承认,自己承认相比不承认等于 从判刑2年改为无罪释放;如果对方承认,自己承认相比不承认相当于从判刑20年减到了10年。这样,对甲乙双方来说,最佳的选择都是承认杀人。
这个结果与他们是否真的杀了人无关,即使他们没有杀人,也会承认杀人。由于特定的选择条件,本来对双方最有利的结局(都不承认杀人,各被判刑2年)不会出 现,出现的是对双方都不利的结果,这就是所谓的“囚犯困境”。我们想想看,“文革”时期坦白从宽、抗拒从严的政策使一大批人承认了自己从没有犯过的“罪 行”,原因就在于此。
“囚徒困境”具有非常深刻的含义,它说明了为什么短视地追求自己利益将导致对大家都不利的结局。现实中类似的例子还很多,比如为了图一时的方便,大家都不 按交通规则行事,结果导致交通瘫痪;再比如前些年很多单位拿国家的钱争相发奖金,结果导致了全社会的通货膨胀。不同的是,在囚徒困境模型里只涉及两个人, 如果这种情况重复出现,两个人很容易从失败中吸取教训,从选择承认杀人改为不承认,这样,处境就可以改善。而生活中很多类似囚徒困境的情况涉及到成千上万 的单位或个人,要想让他们一致地改进策略就非常困难。
在囚徒困境中,双方都承认杀人是一个稳定的结果,因为任何一方一旦单独离开这个选择,只会使自己的处境变得更坏。在多次重复的情况下,双方可能通过吸取教 训改变策略(都不承认罪行),使双方都能受益。然而这又是一个比较脆弱的均衡,因为任何一方一旦突然改变策略,承认罪行,又可以立刻得利。但这种利益也不 会长久,到了下一次,对方必然也承认罪行,从而回到最初对双方都不利的状况。所以,除非双方都能着眼于长远利益,并克服侥幸的心理,他们才可能走出困境。
博弈论的基本概念和分析方法
“囚 徒困境”其实是博弈论里一个特定的例子。博弈论又叫对策论,它研究两人或多人对局时,各方如何决定自己的策略,以求得最佳结果。在博弈中各方都有几种可供 选择的着法,各方虽然知道每种对策所导致的后果,但并不知道对方将选择何种着法。它是对利益对立条件下人的选择规律性的客观研究,它不偏袒任何一方,它既 要考虑如何进攻,又要考虑如何防御。
博奕论中的对局(game),定义为有一定人数参加(不是变换着的)、每人有一定数目的策略(strategy)。各方的策略给定后,称为一个局 (play)。对所有发生的局都有一个支付数量(payoff),就称为对策。下面我们再举一个例子来说明博弈论的分析方法。
设甲、乙二人参加一种游戏,甲有两种选择:A1或A2;乙也有两种选择:B1或B2。游戏规则规定:如果甲选择 A1,乙选择B1,则乙付给甲1元;如果甲选择A1,乙选择B2,甲付给乙1元;如果甲选择A2,乙选择B1,乙付给甲2元;如果甲选择A2,乙选择 B2,甲付给乙2元。我们可以把游戏规则用一个方阵来表示:
这个方阵我们称为甲的支付矩阵,矩阵中的正数表示甲的所得、乙的支付,而负数表示甲的支付、乙的所得。类似地,可以想象,乙也有一个支付矩阵,其中的数字正好跟甲的支付矩阵反号。这样,我们看甲乙二人会如何选择。
对乙来说,最有利的选择是B2,这样他肯定赢钱,至少能得到1元。如果选B1,他不仅不可能赢钱,反而必须付钱。
对甲来说,最有利的结果是A2B1,但他知道,乙不可能选B1,所以他只能选A1,这样能把损失降到最低。
所以,最后的结果是A1B2,甲付给乙1元。对这个结果,双方都没有改进的余地,如果改变策略只能使自己的处境变得更糟,因而都不愿意改变策略,我们称之 为纳什均衡。在例中,对任何一个局,一方的收入等于另一方的付出,参与各方损益之和为零,称为零和对局。容易看出,零和对局的特点一方的支付矩阵为另一方 支付矩阵的反号。
我们知道,经济活动中的商品交换不是零和对局。参与交换的人都能从中得益,所以他们才有参与的积极性。股票市场也不是零和对局。一个正常的股票市场,从总量上看,投资者赚的钱一定大于赔的钱,这是因为股票市场能促进资源优化配置,为社会创造了财富。
前面支付矩阵得到的结果-1(A1B2)还有一个特点,它是所在行中的最小值,又是所在列中的最大值,我们称之为鞍点。当支付矩阵有鞍点时,双方将稳定在这个点上,不再移动。此策略称为博奕对局的稳定解,简称解。
较复杂的博弈方式:混合策略
对于没有鞍点的对局,双方将采取碰运气的方式混合使用各种策略。下面举一个例子:
在这个矩阵中,找不一个点,在所在行中为最小,同时在所在列中为最大,所以它没有鞍点。这个对局没有一个稳定的解。
设想一下,如果甲选择A1,乙将选择B1;如果乙选择B1,甲又会变为A2;如果甲变为A2,乙又会跑到B2;如果乙到了B2,甲又会选择A1……如此往 复,永远找不到一个稳定的解。对这样的对局,双方无法推测对方的策略是什么,因此只能碰运气,混合使用各种策略。
值得注意的是,混合策略也有均衡解,即按概率分配每种策略,使得结局为最优。这种情况可以引用一个案例来说明(本例为讲座后收集补充)。我们来看一个犯罪者与警察的支付矩阵(假定犯罪者在警察休息时一定作案成功,在警察巡逻时作案一定会被抓住):
这个矩阵的数字含义表示:警察巡逻,犯罪者不作案,双方都没有收益也没有损失;警察巡逻,犯罪者作案,警察因抓到罪犯受到表彰,得到效用2单位,罪犯被判 刑丧失效用2单位;警察休息,犯罪者不作案,警察休息的很愉快得到效用2单位,犯罪者没有收益也没有损失;警察休息,犯罪者作案,警察因失职被处分而丧失 效用1单位,罪犯犯罪成功获得效用1单位。这个博弈是没有纳什均衡的。
但是,如果警察知道犯罪者以p的概率选择作案(不作案概率就为1-p),他该怎样采取自己的行动?对警察而言,巡逻的预期效用为0×(1-p)+2p= 2p,休息的预期效用为2×(1-p)-1×p=2-3p。显然,当2p>2-3p即p>0.4的时候,警察最好选择巡逻;反之2p< 2-3p即p<0.4的时候,警察宁愿选择休息。假设警察应以q的概率巡逻(休息的概率就为1-q),那么犯罪者最好的行动是什么?他作案的预期效 用是-2×q+1×(1-q)=1-3q,不作案的预期效用为0×q+0×(1-q)=0。显然,当1-3q>0即q<0.33时,他的理性 选择是作案,反之不作案。在这个博弈中,警察以0.33的概率巡逻0.67的概率休息,犯罪者以0.4的概率作案0.6的概率不作案构成一个混合纳什均 衡。
博弈均衡的一般规律
为了总结求解零和对局的一般规律,我们再来看一个更复杂的例子。以下为甲的支付矩阵(乙的支付矩阵与此反号):
在对局中,甲有4种选择,乙有5种选择,现在来看二人如何选择自己的策略。
甲作选择时,会这么考虑:如果自己选A1,对方为了最大限度降低损失,必然选B5。同理,如果自己选A2,对方必然选B3;如果自己选A3,对方必然选 B1;如果自己选A4,对方必然选B5。比较四个可能出现的结果(表中斜体字):0、4、2、1,对甲最有利的是4,所以甲会选择A2。
乙作选择时,将这么考虑:如果自己选B1,对方为了最大限度受益,必然选A1。同理,如果自己选B2,对方必然选A4;如果自己选B3,对方必然选A2; 如果自己选B4,对方必然选A1;如果自己选B5,对方必然选A3。比较五个可能出现的结果(表中粗体字):9、6、4、8、8,对乙最有利的是4,所以 乙会选择B3。
最后的结果是A2B3——乙向甲支付4,这是一个稳定解(也是纳什均衡),无论甲或乙都不会离开这个策略,因为离开将对自己不利。支付值4有一个特点,它 是各行的最小值中最大者,同时又是各列中最大值中的最小者,这就是鞍点。由此可以得出求解二人零和对局的一般方法:寻找支付矩阵各行中最小值中的最大者 (Maximin),同时寻找各列中最大值中的最小者(Minimax),如果两者重合,重合点就是对局的鞍点,此时我们称之为纯策略的均衡解。
根据支付矩阵横行的Maximin=竖列的Minimax求解零和对局的规律,我们再来回顾前面第一个对局中的求解过程。
在例中,甲选择的每一个策略中都有一个损失最大的。他会比较所有策略中损失最大的结果中选损失最小的。其他策略可能有得益,但是也可能损失更大。如果对方 是聪明的,就不会制造空子。所以甲将在横行中选择策略A1(如果选择策略A2他可能损失2,现在顶多损失1),这是选择最小值中的最大者,即 Maximin。
乙选择策略的原则也类似,他将找出同一支付矩阵各列中的最小者,然后比较这些最小值,找出最大的,即Minimax(也是对他自己的支付矩阵中的 Minimax)如果此结果与甲所选的结果重合,则该对局有解。稳定解所对应的支付值为对局的值。在上例中即为-1(A1B2)。
博弈矩阵中Minimax=Maximin代表最优均衡解的概念有着深刻而普遍的经济学含义。市场均衡中需求和供给的交点即意味着Minimax of demand set(需求方最大值中的最小者)=Maximin of supply set(供给方最小值中的最大者)。我们可以通过供求曲线的相交来说明这个道理。如图:
D 为某商品的需求线,它代表商品的价格越低,愿意购买的人就越多。例如,当价格为16时,购买者为4;价格为13时,购买者为8;价格为10时,购买者为 11……在这里,可以把需求线看作一个连续变动的过程,当价格一点一点降低时,购买者在一点一点增加。需求线上的每一个点,既代表一个价格,又代表一个消 费者的购买量,该价格是该消费者对该商品的最高出价,一旦售价高于此价格,消费者将放弃购买。所以,需求线代表着一组最高出价的集合,此集合中的元素从高 到低排列,就构成了向右下倾斜的需求线。需求线上的每一个点表示最高出价(该点左边的点的集合)集合中的最低价,也就是Minimax.
再看供给线S,它代表商品的价格越高,愿意出售的人就越多。例如,当价格为5时,出售者为6;价格为8时,出售者为9,当价格为10时,出售者为11…… 在这里,同样可以把供给线看作一个连续变动的过程,它意味着当价格一点点上升时,出售者会一点点增加。供给线上每一个点都代表一个出售者的最低售价,如果 价格低于这个水平,出售者将放弃出售。所以,供给线代表一组最低售价的集合,此集合中的元素从低到高排列,就构成了向右上爬升的供给线。供给线上的每一个 点表示最低要价(该点左边的点的集合)集合中的最高价,也就是Maximin.
通过市场交易,最后需求线和供给线的交点将形成均衡点,此时有11(个)人愿意以10(元)的价格购买此商品,同时又有11(个)人愿意以10(元)的价 格出售此商品,市场将完全出清。均衡价格10既是每个购买者最高出价中的最低价,又是每个出售者最低要价中的最高价,这就是我们前面所说的Minimax =Maximin。此时,市场处于稳定状态,且消费者剩余和生产者剩余达到最大,为最优均衡解。
博弈论和信息经济学的简单应用
下面来谈博弈论和信息经济学的一些简单案例。
有一个居民区,由于没有安装街灯,因此带来了很多不便。于是管理部门准备通过集资来解决这个问题。但在管理者向居民们收费的时候,却出现了问题:因为各个 家庭的收入不同,具体情况也不一样:有的上夜班,有的不上夜班,有的家庭老人妇女多,有的都是青壮少年……这样,他们对街灯的需求不相同,管理者也就无法 向他们收取统一的费用。
我们可以想象,其实每个家庭对街灯给自己带来的好处都有一个评价。据此,管理者可以让他们自愿进行出资报价,如果报价之和大于修建街灯的费用,则街灯可以 设置,余款按比例退回出资本人,这样最为公平合理。但是问题在于,由于有搭便车的思想,各个家庭在报价的时候报出的数字往往少于其真实评价。例如,我本来 觉得设置路灯对我的好处能值100元,但我只报60元,我希望自己少出点钱,别人多出钱,而我一样能享受到街灯的好处。这个想法是比较“聪明”,但如果人 人都跟我一样想,街灯就可能因为经费不足无法修建起来。这种情况经常发生。
如何让大家都说真话呢?研究者提出这样的办法:管理者首先要向居民申明,如果报价之和超出修建街灯的费用,余款按出资比例退回,多报多退,少报少退,这样 很大程度上可以减轻大家按真实估价报价的顾虑。但即便这样,仍然可能出现报价不足的情况。这时候要采用多次博弈的方法:在保密条件下重复报价,第一次不行 报第二次,第二次不行报第三次……这样的重复报价对己无损,且因为各家各户都希望街灯能修建起来,所以他们会愿意参与重复报价,并逐渐提高出价,直到凑够 修建费用或达到他们的真实评价为止。
经验表明,上述方法在公共决策问题上能够有效发挥作用,但也有少数情况不能达到目的(例如上面的例子中如果修建街灯的费用超出了居民的预期收益,则无法筹集足够的修建经费)。这就是对策论和信息经济学在现实生活中的一例具体运用。
还有一种关于对策论的研究是对拍卖的研究。一般来说,拍卖有四种方式:英国式、荷兰式、最高价封标拍卖和第二价格封标拍卖。
英国式拍卖是我们最为常见的:由拍卖师从低到高公开叫价,潜在的买主如果认为价格可以接受,就举牌应价。通过买主的竞争,到最后只剩下一个应价者的时候, 买卖双方就按此时的叫价成交。这种拍卖一般都设定最低价,如果连最低价也无人应价,拍卖就中止,并不进行交易。这种拍卖适用于艺术品、土地等时效性不是很 强的商品。
另一种公开叫价的拍卖还有荷兰式拍卖:它由拍卖师从一个相当高的价位开始叫价,从高到低,一旦有第一位卖主接受叫价,就按照这个价格成交。荷兰式拍卖适用于时效性比较强的商品。如鲜花和活鱼这样的商品,不及时脱手不行,因此常采用荷兰式拍卖。
最高价封标拍卖采用书面投标的形式,先由买家分别保密报价,然后公布投标结果,由出价最高的买家购得商品。
第二价格封标拍卖跟上面的最高价封标拍卖类似,不同的是:前者是按最高出价成交,而后者是按次高价成交。举例说:四个人竞购一个拍卖品,甲乙丙丁分别秘密 出价6、7、8、9,开标后,出价最高的丁将按次高的出价8购得拍卖品,这就是第二价格封标拍卖。这种方式非常有利于杜绝侥幸心理,保证买方以对商品的真 实估价参加竞拍。
上述四种拍卖方式各有不同的适用场合。之所以发展出形式众多的拍卖方式,也是出于鼓励传递真实信息的需要,以达到准确估价,价高者得的目的。而有趣的是, 根据对策论和信息经济学的研究:在竞购者行为理性和数目众多等条件下,上述四种拍卖方式导致的拍卖人的预期收入都是相等的。或者说,四种拍卖的效率都是相 同的。
补充总结
最后我们来回顾一下囚犯难题所体现的深刻意义。囚徒困境的特点,是博弈双方互不信任,采取损人利己的策略,最后导致对双方都不利的结局。这个例子可以很好地说明道德的特点和它产生的过程。
道德的特点是人人遵守、人人受益,但它可能需要牺牲个人的短期利益。曾经有学者指出,人和动物的区别,不是使用工具或使用语言,而是人有道德,知道通过抑 制短期利益获取长期利益。最初,人跟动物一样,是在野蛮争斗的“丛林规则”中生存。后来,通过重复博弈和长期学习,人们意识到道德的重要性,把道德秩序建 立起来,才使人真正从动物世界中分离出来。这一过程了经历很长的时间。
道德的建立非常困难,而它的破坏却很容易。因为在大家都遵守道德的时候,个别人不讲道德反而能获益。例如在马路上,大部分车辆都按顺序行驶,一旦个别车辆 加塞插队,它就能比别人走得快。此时如果守规矩的车觉得吃了亏,也会跟着不守规矩。大家都不守规矩,都加塞排队,就等于道德完全失效。结果如何?不仅没有 人能走得快,反而会使交通陷于瘫痪,大家都走不了。所以缺乏道德的状态也不会一直持续下去,新的道德秩序终究会建立起来。道德就是在反复试错和淘汰的过程 中不断发展的。
专门的研究还表明,在社会发展的长久历程中,道德状态并不完善,往往是大部分人能遵守道德,小部分人道德败坏,但在一定限度内,社会的稳定和发展不会遭到破坏。这说明道德秩序是一个连续性变量。
这是一个非常重要的结论。它告诉我们:道德水平的提高不是一蹴而就的,良好的道德风尚要靠每个人的行动一点一点去积累。特别在整个社会风气恶劣的时候,我 们不能光抱怨别人,而应该从自己做起,从身边做起,奉行良好的道德规则。这样,每多一个讲道德的人,我们的社会就会朝好的方向转变一步。
 爱华网
爱华网