分类:
系统聚类方法(Hierarchical Cluster过程):直观、易懂
快速聚类(K-means Cluster过程):快速、动态
有序聚类:时间顺序or大小顺序
相似性度量:
一。变量测量尺度的类型
间隔尺度:数量概念
顺序尺度:次序概念
名义尺度:纯粹一个标记,例如眼睛颜色、物品种类
二。样品间亲疏程度的测度
1.
R型聚类:(P阶X'X)基于样品,对指标聚类——相似系数(1,-1)
Q型聚类:(n阶XX')基于指标,对样品聚类——将样品看成点,点点距离
2.常用距离算法
闵可夫斯基距离(明氏距离minkowski):闵氏距离、绝对距离、欧式距离、切比雪夫距离
——受量纲影响,没考虑变量之间相关性
马氏距离(广义欧氏距离)
——不受量纲影响,考虑了变量之间相关性(假设变量之间独立)
兰氏距离
——不受量纲影响,没考虑变量之间相关性
斜交空间距离
3.相似系数(变量相似性度量)
相似系数:数据便准话后的夹角余弦
夹角余弦
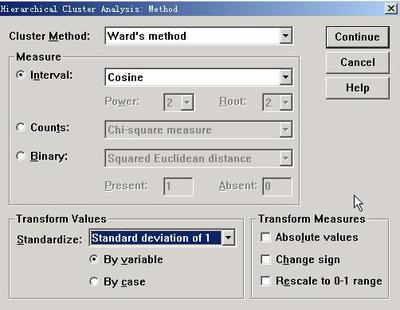
系统聚类方法
一。分析过程
每个样本自成一类,计算两两距离,共有Cn2个——将距离最小的合并为新类——利用递推公式计算新类与其他类之间的距离——重复,直到所有样本点归为一类——画聚类图——决定类的个数
二。常见聚类法
最短距离(nearest neighbor)
最长距离(furthest neighbor)
中间距离法
重心法(gentroid clustering):样品的均值法
离差平方和法(ward's method):类内离差平方和最小,类间最大
三。确定类的个数
1.给定阈值:距离<阈值
2.观测样品散点图
3.R^2统计量=类间离差平方和总离差平方和——越大越好
4.伪F统计量(Pseudo statistic)——越大越好
5.伪t^2统计量:评价第p类和第q类合并的效果(与没合并时比较)
四。主要步骤
1.选择变量
2.计算相似性
3.聚类:选择方法,确定类数
4.聚类结果的解释和证实
动态聚类
一。思想
主要作用是适用于大型数据。克服了系统聚类的复杂繁琐。
二。方法:
K-meanscluster:空间群点任选两点聚核——第一次分类——求该类中心——第二次分类——……直到所有样品不能再分配为止
三。特点
效率高:收敛到局部最优解
四。问题
分类型数据中心如何定义
预先指定聚类个数K
结果受初始值的影响
适合形状规则的聚类
 爱华网
爱华网