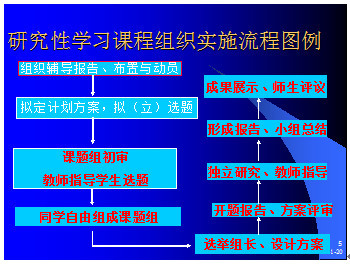
数字是人类生活的工具,但我国的数学教学特别是高中数学教学仍未真正跳出应试教育的模式,教学中,重“知识”轻“能力”, 重“考试”轻“实践应用”. 新课程标准倡导发展学生的应用意识,强调自主探索、合作学习,力求使学生体验数学在解决实际问题中的作用,数学与日常生活及其他学科的联系,把研究性学习又提到了新的高度. 为此我和本校的教师一起承担了宁波市基础教学研究立项课题———在生活中“寻找”数学. 在本课题的实施过程中发现:现代学生数学实践的应用意识,应用能力,应用现状相当薄弱,特别是如何从实际生活中发现问题并归结为数学模型,即在研究性学习中如何选题,如何提出问题方面尤为薄弱. 在实施课题中,我们通过问卷调查,交流对话,开设讲座,系列板报,网络查寻,阅读自学,合作交流,自主探索,动手实践,知识竞赛,数学建摸等各种生活中“寻找”数学的活动,发展学生的数学应用意识,体会数学的应用价值,逐步帮助学生认识到:数学与我有关, 与实际生活有关,数学是有用的,我要用数学,我能用数学. 发现了大量数学应用的事例,开阔了学生的视野. 为新课程高中数学研究性学习如何选题,提供了大量的素材,现将“寻找”数学的结果整理如下.
1 高中数学研究性学习课题的类型及来源
1.1 社会生活实践方面
(1) 我们喝易拉罐的时候 , 有没有想过怎样制作,容积大且用料省,根据你的研究,可以向易拉罐生产厂提何建议 ?类似的有无盖盒子的最大容积问题:用一张边长为 a的正方形铁皮,如何制作一个无盖长方体盒子,使其容积最大 ?
(2) 当你在阳台晒太阳时有没有想到商品房楼高,楼间距与光照的关系,能用数学和地理知识推导出公式来表示吗 ?从而得出对 n 层商品房而言后排一层,二层的阳台要照到太阳,阳台到前排楼房最小距离吗 ?
(3) 在开、关窗户时 ,想过窗户的面积与采光量的问题吗 ?烈日下,你想过遮阳棚搭建方式与遮挡太阳光线的效果有关吗 ?糖水中为什么糖放的越多糖水就越甜 ?能用数学知识解释吗 ?
(4) 我们早晨起床刷牙用的牙膏的包装有大有小. 其价格也不相同,你想过大小包装与其价格之间的关系吗 ?除了牙膏以外,其它商品都有大小包装之分,如饼干、瓜子、食油等等. 你吃东西时,想过营养成份的搭配吗 ?它们都与数学有关系.
(5) 现在很多人家都安装了太阳能热水器 , 请你用所学的数学等知识说明在各个不同季节,热水器太阳能接受器安放的倾斜角多大时,可使正午时阳光直射热水器,从而取得最大热效率. 根据你的研究,你可以向热水器生产厂提何建议 ?
(6) 洗衣服是我们生活中最平常不过的事情 ,但从中可得出一个研究性课题. 探讨全自动洗衣机在洗衣时用水设计中的数学原理: ①为什么设计成等量注水 ?②分 3 次注水的合理性是什么 ?
(7) 在公路的一侧从 A 至 B 有一排楼房 , 想在公路 L 上的任何一处拍一张正面照,如何选择公路上的点,使拍摄的一排楼房的取景最大 ?(点 A 与点B 与直线 L 的各种位置关系讨论. )
(8) 调查电 , 煤气 , 煤的价格 , 使用电和煤气 ,煤,到底哪个更合算 ?
(9) 十字路口交通流量与红绿灯时间设置关系,根据你的调查向公路交通部门提合理化建议.
(10) 正弦、余弦定理在日常生活中的应用 , 如小河对岸两点间长度, 楼房, 电视塔等高度测量问题.
(11) 衣服的价格、质地、品牌 , 左右消费者观念多少 ?
(12) 日常生活中的悖论问题.
(13) 水库的来水量如何计算 , 统计本地区的月降水量。
(14) 调查各镇中学生生活学习情况 , 向学校等教育部门提合理化建议.
(15) 调查城镇 / 农村消费、饮食构成及优化设计.
(16) 出租车车费的合理定价.
(17) 数学中的最优化问题应用.
(18) 黄金数的广泛应用.
(19) 气象学中的数学应用问题.
(20) 教育储蓄与教育保险比较.
1.2 体育活动方面
(1) 姚明在 NBA 的投蓝命中较高 ,为什么跳得越高投篮就越准,怎样用数学知识来解释.
(2) 足球运动员在射门时 ,面对对方守门员 , 射门时的角度、球速与守门员扑球时的移动速度有何关系,怎样能将球射入球门 ?足球运动员在何处射门最好(不考虑其它因素) ?类似问题有灯的位置与照明度的关系,上课时,坐在什么位置才能最清楚的看到黑板的问题.
(3) 推铅球 ,扔实心球 ,抛垒球时什么样的角度出手最好,用数学知识来验证.
1.3 商业经济问题
(1) 轿车已进入很多家庭 , 调查各种家用轿车价格,养路费,保险费,燃料费,维修费等费用,计算轿车的最佳使用年限,及在家庭开支中的比例,如何优化家庭消费结构.
(2) 调查报亭卖报情况(进价、售价及卖不出去而退回每份报纸赔钱多少) 统计一个月的销售情况,为报亭主人决策,使之收益最大.
(3) 调查保险公司养老保险险种及分红方法 ,某人在 40 岁时参加保险,或将应交保额逐年存入银行,假设此人预期寿命为 75 岁,请你对这两种投资方式进行比较,确定此人是投保收益大,还是存银行收益大.
(4) 购房贷款决策问题. ( 通过调查银行利率 ,利税及房价决定哪种方式购房划算.)
(5) 调查附近工厂或商店进货,生产,销售情况,运用线性规划知识进行合理调派,使之利润最大化?
(6) 投资人寿保险和设资银行的分析比较
(7) 通讯网络收费调查统计 , 选择什么手机服务会更合适 ?家里使用市内电话,小灵通选择什么服务最省钱,设计一个方案.
(8) 证券投资中的数学.
(9) 用数学眼光看“养老金”问题.
(10) 中国体育彩票 ,电脑福利彩票中的数学问题.
(11) 如何合理抽税.
(12) 环境规划与数学.
(13) 调查某种商品的销量与它的利润的关系 ,并决策如何可使其获利最大 ?
(14) 银行存款利息和利税的调查 , 怎样存款能获利最多.
1.4 函数建模方面问题
一个例子:某工厂今年 1 月、2 月、3 月生产某种产品的数量分别为 1 万件,1.2 万件,1.3 万件,为估测以后每月的产量,以这三个月的产品数量为依据,用一个函数模拟该产品的月产量 y 与月份 x 的关系,模拟函数选用二次函数或函数 (其中a, b, c 为常数) ,已知 4 月份该产品的产量为 1. 37 万件,请问:用以上哪个函数作为模拟函数较好,说明理由 ?
(1) 调查当地耕地面积的变化情况 , 预测今后的耕地面积.
(2) 以本班期中考试的数学和物理成绩为样本,研究同学们物理成绩与数学成绩间是否存在一定的关系,并用我们学过的函数进行拟合.
(3) 对当地或国家近年来人口增长的情况调查,预测今后人口数量,给政府提出几点建议.
(4) 建立“肯德基”(或其它) 商标的函数关系式(可用分段函数表示) .
(5) 气象学中的数学问题 (温度、湿度、空气污染指数、臭氧层的变化) .
(6) 验证物体在常温下温度变化的冷却模型 , ( 其中θ1 为物体的初始温度 ,θ0是环境温度,θ为时间t 后物体的温度,其中 k为正的常数) . 再探索以下问题: ①一杯开水冷却到常温大约需要的时间 ?②冰箱里的肉拿出来解冻要多少时间 ?③在寒冷的冬季,是冷水容易结冰,还是热水容易结冰 ?
1.5 深入研究教材 ,从教材中取得课题
(1) 人教社最新出版的教材中几乎在每一章节后都安排了阅读材料或实习作业或研究性课题,其中阅读材料往往是对本章知识的产生和发展作简要的介绍,可以要求学生通过网络、图书馆、专家访谈等方式,收集资料,作出一个详细的报告;实习作业往往给一种思路,要求同学根据这个思路,自己提出一个问题,设计解决方案,调查收集数据,分析解决问题;而研究性课题给出了研究内容,要求学生展开研究并得出结论. 这些都是开展研究性学习的很好的内容.
(2) 从拓宽知识面选择内容 :
( a) 函数 f ( x) = ax + b/x ( a, b为待定常数) 的性质研究. (可利用几何画板结合研究.)
( b) 斐波那契数列研究 ( 从免子的繁殖等实际问题建立递推数列问题) ,通过对递推数列的相关知识进行研究性学习,不仅可以巩固等差等比数列的相关知识,更能学会变换、转化等思想方式,培养创新思维和能力.
( c) 研究等“和”数列与等“积”数列 (其定义与等差、等比数列类似) 的通项与性质.
( d) 课本定义球面距离为“:在球面上, 两点间的最短距离,就是经过这两点的大圆在这两点间的一段劣弧的长度, 我们把这个弧长叫做这两点的球面距离.”两点的球面距离为何最短,教材并没有说明,这一问题也是进行研究性学习可选择的较好内容.
(3) 从平时习题 ,例题 ,及高考试题的推广和变式选择内容.
( a) (2001 年全国高考试题改编) 设 f ( x) 是定义在 R上的偶函数,其图象关于直线 x = 1 对称,证明 f ( x) 是周期函数. 让学生进行多方面的研究来发现抽象函数周期性,奇偶性,对称性之间的关系.
( b) 在学完圆锥曲线这一章后 , 可提出研究性课题“:抛物线的焦点弦的性质研究”和“圆锥曲线的焦点弦的性质研究”.
1.6 其他方面
(1) 向量在物理中的应用.
(2) 地理中的大气环流 ,风向中的数学知识.
(3) 圆锥曲线光学性质.
(4) 多媒体辅助教学在数学教学中的作用调查.
(5) 编程中的优化算法问题.
(6) 利用“几何画板”对函数的性质的研究.
(7) 用“几何画板”研究最值问题.
(8) 用“几何画板”研究动点的轨迹问题.
(9) 编程解一元二次方程.
(10) 数学对计算机发展的贡献.
(11) 对我们学习数学有帮助的电脑软件及其特点.
(12) 制作较为复杂的数据统计表格与分析软件.
(13)“开放型题”及其思维对策.
(14) 直角三角形在实际中的应用.
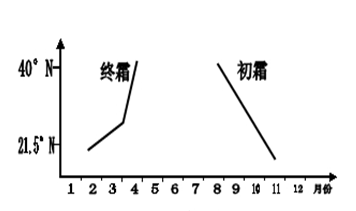
(15) 天气预报、台风警报、空气质量状况预报的数学知识.
(16) 多面体欧拉定理的发现.
(17) 编程关于组合购房贷款等额还款计算.
(18) 数学的发展历史.
(19) 关于数学知识在物理上的应用探索.
(20) 零件供应站(最省问题) .
设在一条流水线上有 5 台机器工作,我们要在流水线上设立一个检验站,经检验合格后才能进行下一道工序,若 5 台机器的工作效率相同,问检验台放在何处可使移动零件所走的距离之和最小 ?(所花的总费用最省) 如果是 n台呢 ?(可以用平面几何知识,也可以建立函数关系式,作出图象讨论得出) 若5 台机器的效率不同又如何呢 ?
(21) 高中数学的学习活动 ———解题后的反思———开发解题智慧.
(22) 如何计算一份试卷的难度与区分度.
2 高中数学研究性课题选题的原则
(1) 问题性原则 ,问题是科学思维的起点 , 通过数学建模活动引导学生从实际情境中发现问题,并归结为数学问题,尝试用数学知识和方法去解决问题.
(2) 价值性原则 , 价值性主要表现为它的科学性、需要性和创造性,能否促进学生数学应用能力的发展和提高.
(3) 可操作性原则 , 选择的课题要适合中学生的知识水平和能力及相关物质条件.从科学研究的意义上讲,发现问题比解决问题更重要,它是学得真知的关键一步,一个人在学习的过程中,假如提不出问题,那么就很难想像他真正地学到了什么. 生活中处处留心皆数学,关键是我们怎么去发现它,让我们发现并研究这些数学问题吧 !相信你会其乐无穷.
参考文献
1 兰永胜主编. 数学思想方法与建模技巧. 青岛 :青岛海洋大学出版社
2 戴再平主编. 高中数学开放题集.
3 秋森著. 数学问题与模式探求. 上海 :华东理工大学出版
 爱华网
爱华网