《一笔画》教学设计
教学目标:
1、理解一笔画的特点,知道怎样的连通图可以成为一笔画。
2、会将一笔画问题的解决方法应用于实际。
3、激发学生学习数学的兴趣,培养学生的创新能力和应用意识。
教学重、难点:
“一笔画”问题的解决方法。
教学用具:实物投影仪
教学过程:
一、引入:
(投影出示)哥尼斯堡七桥图。
师:有谁能说说这副图画了什么?(学生口答)
师:有没有同学知道这副画所展现的情景引发了一个怎样的数学问题?
师(简介七桥问题):它一直困扰了人们很多年,直到1836年,大数学家欧拉用一个简单的数学知识给出了结论:不可能!同学们你们知道欧拉是用什么知识解决了这个数学问题的吗?就是一笔画!(板书课题)
师:什么是一笔画,谁能说说?连续而不重复(板书)那么欧拉是怎样用它解决了七桥问题的呢。今天就让我们追寻着欧拉的脚步一起来研究这个问题。
二、新课:
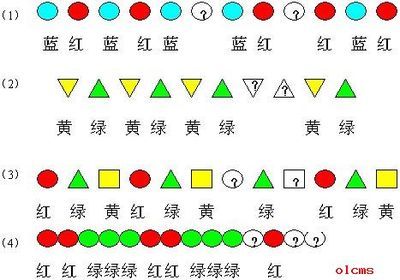
1、(出示图1)师:这些都是我们常见的图能一眼看出那些图有可能是一笔画吗?为什么?
2、师:像这样各部分连在一起的图,我们称为连通图。连通图是由什么组成的?
(学生口答,教师归纳:点和线)
3、师:我们把与奇数条线相连的点称作奇点。(板书)与偶数条线相连的点称为偶点。(板书)每副连通图都是由点和线组成的,就会出现奇点和偶点。那么怎样表示连通图中的点呢?请同学们看例题(出示图2)用“2”表示偶点,用“1”表示。(教师示范,学生试做)以后我们在研究连通图时就可以先标出图中的奇偶点,再进行研究。
4、师:我们已经了解了有关连通图的知识,也知道只有连通图才能一笔画,那么是不是所有的连通图都能一笔画呢?请大家在练习本上将1、2、4、5四个图画下来,再用铅笔画一画,用箭头表示方向。
5、师:同学们画得怎么样,连通图是不是都能一笔画?(学生展示画法)
师:能一笔画的图有什么特点,请同学们继续进行研究,看看会有什么发现。(学生探究,教师参与)
师:有什么发现吗?(生口答)那么不能一笔画的图呢?(生口答)
6、师:通过刚才的研究同学们都有了自己的发现,(师初步口头小结)下面让我们通过课本上的几个图来验证我们的发现是否正确。(学生完成后展示并说明)
师:能总结一下什么样的连通图能一笔画吗?(学生口答)教师小结板书:两个奇点、全都是偶点。
三、展开:
1、(出示村庄图)师:能不能既不重复又不遗漏的走遍每一条路?能很快做出自己的判断吗?(生口答)动笔画一画,验证一下。(完成后展示)
师:这些路线图的出发点和终点有没有共同点?(生口答)
教师板书:由一个奇点出发回到另一个奇点。
2、(出示城市图,教师简述情景)师:能说说他会是在研究什么呢?(生说)
师:我们有办法帮助他吗?(生说)可是这里地点那么多,道路这么复杂,小张怎样才能很快地熟悉工作环境呢?请大家先帮他解决这个问题。(学生完成,教师指导)
师:有办法了吗?(学生,教师共同展示设计的连通图)
师:有了连通图就能解决问题了吗?请大家继续帮助他。(学生完成,教师参与)
师:能实现小张的愿望吗?(学生展示,讲解)
师:我们有很多种路线供小张选择,这些路线图有共同点吗?(生思考,交流后口答)教师小结板书:从起点回到起点。
3、师:看来一笔画的确可以让复杂的问题简单化,提高效率。那么,现在我们能解决著名的“七桥问题”吗?(学生完成,展示交流)
师:看来只要我们用数学的眼光观察生活,用数学的思维解决生活中的问题,我们每个同学就都有成为大数学家的潜能。
四、应用:
师:最后请同学们根据自己的生活实际,将自己常去的场所设计成能既不重复又不遗漏的走遍每一个场所的连通图,想想可以怎样设计。
板书:
一笔画
连续而不重复
奇点偶点
两个奇点从一个奇点回到出发回到另一个奇点
一笔画
都是偶点从起点回到起点

 爱华网
爱华网