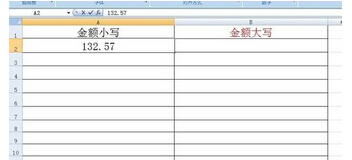
Two-sample F-test for equal variances
Syntax
H = vartest2(X,Y)
H = vartest2(X,Y,alpha)
H = vartest2(X,Y,alpha,tail)
[H,P] = vartest2(...)
[H,P,CI] = vartest2(...)
[H,P,CI,STATS] = vartest2(...)
[...] = vartest2(X,Y,alpha,tail,dim)
Description
H = vartest2(X,Y) performs an F test of the hypothesis that two independent samples, in the vectors X and Y, come from normal distributions with the same variance, against the alternative that they come from normal distributions with different variances. The result is H = 0 if the null hypothesis (variances are equal) cannot be rejected at the 5% significance level, or H = 1 if the null hypothesis can be rejected at the 5% level. X and Y can have different lengths. X and Y can also be matrices or n-dimensional arrays.
For matrices, vartest2 performs separate tests along each column, and returns a vector of results. X and Y must have the same number of columns. For n-dimensional arrays, vartest2 works along the first nonsingleton dimension. X and Y must have the same size along all the remaining dimensions.
H = vartest2(X,Y,alpha) performs the test at the significance level (100*alpha)%. alpha must be a scalar.
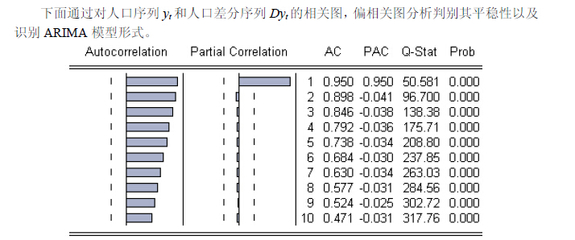
H = vartest2(X,Y,alpha,tail) performs the test against the alternative hypothesis specified by tail, where tail is one of the following single strings:
'both' — Variance is not Y (two-tailed test). This is the default.
'right' — Variance is greater than Y (right-tailed test).
'left' — Variance is less than Y (left-tailed test).
[H,P] = vartest2(...) returns the p-value, i.e., the probability of observing the given result, or one more extreme, by chance if the null hypothesis is true. Small values of P cast doubt on the validity of the null hypothesis.
[H,P,CI] = vartest2(...) returns a 100*(1-alpha)% confidence interval for the true variance ratio var(X)/var(Y).
[H,P,CI,STATS] = vartest2(...) returns a structure with the following fields:
'fstat' — Value of the test statistic
'df1' — Numerator degrees of freedom of the test
'df2' — Denominator degrees of freedom of the test
[...] = vartest2(X,Y,alpha,tail,dim) works along dimension dim of X. To pass in the default values for alpha or tail use [].
Example
Is the variance significantly different for two model years, and what is a confidence interval for the ratio of these variances?
load carsmall
[H,P,CI] = vartest2(MPG(Model_Year==82),MPG(Model_Year==76))
 爱华网
爱华网