跳转到: 导航, 搜索
Β函数,又称为贝塔函数或第一类欧拉积分,是一个特殊函数,由下式定义:
其中 。
目录
[隐藏]
1 性质 2 伽玛函数与贝塔函数之间的关系 3 导数 4 估计 5 不完全贝塔函数 5.1 性质
6 参见 7 参考文献 8 外部链接
[编辑] 性质
Β函数是对称的,也就是说:
它有许多其它的形式,包括:
其中 是伽玛函数。
就像伽玛函数描述了阶乘一样,我们也可以用贝塔函数来定义二项式系数:
[编辑] 伽玛函数与贝塔函数之间的关系
为了推出两种函数之间的关系,我们把两个阶乘的乘积写为:
现在,设 , ,因此:
利用变量代换a = rcosθ和b = rsinθ,可得:
因此,有:
[编辑] 导数
贝塔函数的导数是:
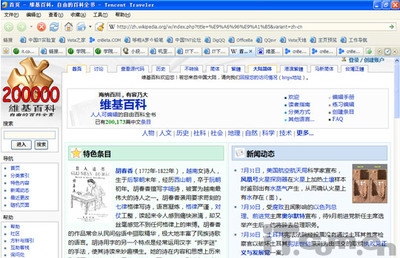
其中ψ(x)是双伽玛函数。
[编辑] 估计
斯特灵公式给出了一个用来近似计算贝塔函数的公式:
[编辑] 不完全贝塔函数
不完全贝塔函数是贝塔函数的一个推广,把贝塔函数中的定积分用不定积分来代替,就像不完全伽玛函数是伽玛函数的推广一样。
不完全贝塔函数定义为:
当x = 1,上式即化为贝塔函数。
正则不完全贝塔函数(或简称正则贝塔函数)由贝塔函数和不完全贝塔函数来定义:
当a和b是整数时,计算以上的积分(可以用分部积分法),可得:
[编辑] 性质
[编辑] 参见
贝塔分布 二项分布 伽玛函数
[编辑] 参考文献
M. Zelen and N. C. Severo. in Milton Abramowitz and Irene A. Stegun, eds. Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables. New York: Dover, 1972. (See §6.2, 6.6, and 26.5) W. H. Press, B. P. Flannery, S. A. Teukolsky, W. T. Vetterling. Numerical Recipes in C. Cambridge, UK: Cambridge University Press, 1992. Second edition. (See section 6.4) PlanetMath上用拉普拉斯变换来计算贝塔函数的资料。
[编辑] 外部链接
贝塔函数计算器 不完全贝塔函数计算器 正则不完全贝塔函数计算器
取自“http://zh.wikipedia.org/zh-cn/%CE%92%E5%87%BD%E6%95%B0”
2个分类: 特殊超几何函数 | 伽玛及相关函数
 爱华网
爱华网